Raycasting学习记录
前言
我是一个电子游戏爱好者,对市面上各种类型的电子游戏都稍有涉猎,其中最喜欢的应该就是射击游戏
凭借着对游戏的喜爱,我曾经追溯过游戏发展的历史,尤其是我最感兴趣的射击游戏:按照时间年表从现在到过去,《Splatoon》将游戏机制与手柄操作完美结合,定义了新的手柄射击方式;《Counter-Strike》这部里程碑式的作品将多人对抗竞技发扬光大;《Half-Life》让游戏不再局限于射击体验,而在流程中更加着重于剧情与解谜成分;《GoldenEye 007》和《Halo》把射击游戏搬上了主机平台,优化了手柄的操作;《Quake》,世界上第一款实时3D渲染的射击游戏,第一款真正意义上的3D射击游戏;《Doom》和《Wolfenstein 3D》,利用伪3D的技术,超越了世代技术力的限制,让第一人称射击游戏提前出现了许多年
我其实在查资料的时候就很疑惑,毕竟我没有亲自经历过电子游戏发展早期的那个时代,既然机能不足,不能够支撑3D,那这个所谓的伪3D是个什么东西?
带着这个问题,我就进一步寻找答案,最终找到了叫做Raycasting的技术,这正是当年约翰卡马克在《德军总部3D》和《DOOM》中使用的算法
这是一篇Raycasting教程的博客,质量很高:Raycasting (lodev.org)
更令我惊喜的是,这个算法并没有想象中那样复杂,在复现完以后,我能明确的说:只要有初中几何的知识,以及掌握最简单的二维矩阵乘法知识,就可以复现出这个算法
正好,在计算机图形学的实验课上有足够的时间学习和复现这个算法,毕竟“实验课想做啥就做啥”
于是,带着对射击游戏祖师爷《德军总部3D》的致敬和好奇,我复现了这个经典游戏的基本框架
此篇博客后续内容:Raycasting学习记录_进阶与扩展,增加地板天花板纹理、鼠标控制视角、decoration的Sprite绘制、《白色相簿2》立绘Sprite的绘制,都是在此博客的基础上添加的新内容
源代码和可执行程序已经部署到github上:Raycasting
Raycasting
简介
Raycasting is a rendering technique to create a 3D perspective in a 2D map. Back when computers were slower it wasn't possible to run real 3D engines in realtime, and raycasting was the first solution. Raycasting can go very fast, because only a calculation has to be done for every vertical line of the screen. The most well known game that used this technique, is of course Wolfenstein 3D.
利用Raycasting算法做的游戏是很有时代特色的,比如这样的:

一切可交互的物体,如敌人和物品,都用Sprite贴图来显示,交互逻辑也是很简单的“射爆”
可惜这次复现并没有涉及到Sprite,不过今后肯定会补上的
基本原理,一张动态图就能很好地解释:

用一个二维数组存储地图,0代表可以行走的地面,正数值可以代表不同的墙体,并且可以区分对应不同的纹理
从人物视角发出屏幕宽度像素个数的光线(比如大小是1440*900,就发射出1440道光线),每到光线发射出去后会检测墙面碰撞,如果碰到了墙面,就会记住对应的距离,然后根据近大远小的原理,在屏幕上画出对应高度的线,这个高度就代表墙的高度
比如一道光线碰到了墙,光线长度是5,我们就可以在屏幕对应位置画出\(\dfrac{屏幕高度}{5}\)这么长的线,就代表墙高\(\dfrac{屏幕高度}{5}\);另一道光线碰到了墙,光线长度是10,我们就可以在屏幕对应位置画出\(\dfrac{屏幕高度}{10}\)这么长的线,就代表墙高\(\dfrac{屏幕高度}{10}\)。因此,在屏幕上显示的墙就很符合近大远小的特点:距离近的墙显示就大,距离远的墙显示就小
至于如何计算光线碰到墙的距离,就可以利用DDA算法,具体会在后面的“复现”解释
最基本的复现
本次复现使用SFML多媒体库,原因是我之前用过,比较熟悉,还很简单
最基本的复现,指基础的Raycasting,不涉及纹理和小地图等
可在这里查看源代码
下面是每个部分具体实现的讲解
必要参数声明
此处定义屏幕大小,地图大小,地图
还有玩家位置,视野,面朝方向这些参数
1 |
|
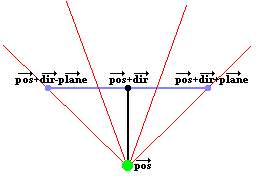
参考原教程,人物的视野范围可以用\(\overrightarrow{pos}\),\(\overrightarrow{dir}\)和\(\overrightarrow{plane}\)组合求得,如图所示,上面代码的对应6个变量就是设置这三个向量用的
关于计时:变量 time 和 oldTime
用于存储当前帧和前一帧的时间,这两者之间的时间差可以用来确定当按下某个键时应该移动多少(无论帧的计算需要多长时间,都能保持恒定的速度),即用于求移动速度和旋转速度
main函数的结构
根据SFML库里介绍的,SFML最基础的main程序结构如下:
1 | int main() |
SFML每次都会重新画一帧,因此需要每一帧调用window.clear();函数
我们要做的,就是每一帧都在屏幕对应位置上画出对应的线
Raycasting的main函数如下:
1 | int main() |
在创建窗口后,就是经典的main函数死循环,每一帧判断是否关闭,然后清除所有图形,重新画新的,再显示到屏幕上
用于画图形的是DDA_algorithm(window)
Move(window)函数是控制角色移动的,会改变\(\overrightarrow{pos}\),\(\overrightarrow{dir}\)和\(\overrightarrow{plane}\)三个向量
紧接着介绍对应的两个函数
DDA_algorithm函数
函数的定义如下
1 | void DDA_algorithm(RenderWindow& window) |
需要传递进main里面声明的window窗口
再看看原理图:

由于每一帧都需要从人物视角发出屏幕宽度像素个数的光线,每到光线发射出去后会检测墙面碰撞,再把对应的长度的墙画在屏幕上
所以这个函数就是一个x从0遍历到screenWidth的循环,每一个x都对应着一个屏幕像素的横坐标,这样我们就有了给竖直线定位用的横坐标,所以这个程序的大致结构如下:
1 | void DDA_algorithm(RenderWindow& window) |
比如,窗口大小设置为1440*900,对应就是1440根光线执行注释里对应的5个操作,然后对应位置画竖直的线,就能达到伪3D的效果
下面将对应注释中的5个操作,介绍具体过程
角色发出光线
需要定义光线的方向,过程如下图

定义光线向量为\(\overrightarrow{rayDir}\),这个向量就可以通过\(\overrightarrow{dir}\)和\(\overrightarrow{plane}\)两个向量求得 \[ \overrightarrow{rayDir}=\overrightarrow{dir}+对应倍数\cdot\overrightarrow{plane} \]
这个倍数的范围应该是在\([-1,1]\)上,这样就能全面覆盖所有视野范围
至于倍数的确定,就需要用到x了:把x这个变量映射到\([-1,1]\)上,对应图上的图,映射得到的倍数命名为cameraX
\[
cameraX=\dfrac{2}{screenWidth}\cdot x-1
\] 所以对应的\(\overrightarrow{rayDir}\)就能求出来,代码对应如下:
1 | //calculate ray position and direction |
DDA算法
必要的变量定义与计算
需要定义几个变量用于计算发出光线碰到墙后的长度
1 | //which box of the map we're in |
mapX和mapY是现在角色所在地图的位置
sideDistX和sideDistY是光线从起始位置到第一个X边和第一个Y边需要行进的距离,可能文字无法精确描述,可以看看图里的定义
deltaDistX是光线从一个X边到另一个X边需要行进的距离
deltaDistY是光线从一个Y边到另一个Y边需要行进的距离
看图就会更容易理解:
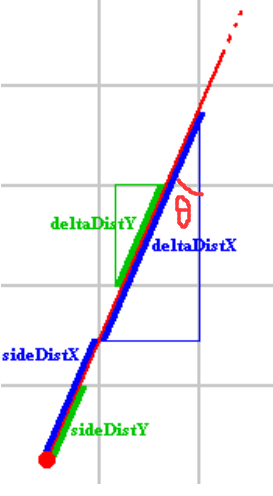
对于一个给定的方向\(\overrightarrow{rayDir}\),对应的deltaDistX和deltaDistY是固定的
设图上的角度为\(\theta\)
推导过程如下: \[ \begin{align*} \tan{\theta}=\frac{rayDirX}{rayDirY}&=\frac{1}{\sqrt{deltaDistX^2-1}}\\\\ deltaDistX&=\sqrt{\frac{rayDirX^2+rayDirY^2}{rayDirX^2}}\\\\ &=\left|\frac{|rayDir|}{rayDirX}\right|\\\\\\ 同理,deltaDistY&=\left|\frac{|rayDir|}{rayDirY}\right| \end{align*} \] 分子的\(|rayDir|\)是模长的意思,而整个式子外面的符号是绝对值的意思
但因为DDA算法只与deltaDistX和deltaDistY的比例有关,所以可以把两个deltaDist化简为:
\[
\begin{align*}
deltaDistX&=\left|\frac{1}{rayDirX}\right|\\\\
deltaDistY&=\left|\frac{1}{rayDirY}\right|
\end{align*}
\]
注:
- 如果不进行化简,就会导致
deltaDist考虑到光线的实际长度,而deltaDist这个变量会用于sideDist的计算,进而用于求出画线长度变量perpWallDist的计算;说人话就是使用公式\(deltaDistX=\left|\dfrac{|rayDir|}{rayDirX}\right|\)和\(deltaDistY=\left|\dfrac{|rayDir|}{rayDirY}\right|\)计算,就会导致墙的高度考虑了光线起点与终点的欧氏距离,会产生“鱼眼效应”,详情见这里 - 化简之后,从计算方法上可以避免产生“鱼眼效应”,因为把
deltaDist缩放了|rayDir|,在计算过程中可以使perpWallDist的值刚好等于sideDistX - deltaDistX或者sideDistY - deltaDistY,很神奇吧 - 还得注意,这种计算方法只是“避免”产生鱼眼效应,而不是“修正”鱼眼效应,这两个是完全不同的概念
- 具体证明“为什么能避免鱼眼效应”见这里
- 如果想看产生“鱼眼效应”的效果,见这里,
只要不嫌晕
但是需要注意,如果方向垂直于坐标轴,比如:
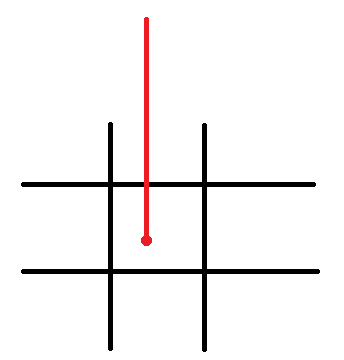
此时的rayDirX = 0,所以给deltaDistX赋值为无穷,比如1e30,Y方向同理
所以就有了对应的代码:
1 | double deltaDistX = (rayDirX == 0) ? 1e30 : std::abs(1 / rayDirX); |
再定义一系列新变量:
1 | //what direction to step in x or y-direction (either +1 or -1) |
stepX,光线方向在X的正负方向,+1代表正方向,-1代表负方向(规定向右为正)
stepY,光线方向在Y的正负方向,+1代表正方向,-1代表负方向(规定向上为正)
hit,检测光线是否撞墙,用于结束循环
side,当光线撞到X方向的墙时,赋值0;当光线撞到Y方向的墙时,赋值1
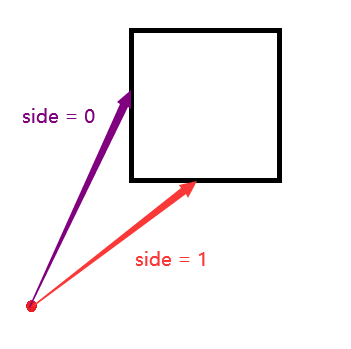
计算sideDist,这个需要自己动手在纸上画一画,就是初中的相似三角形知识
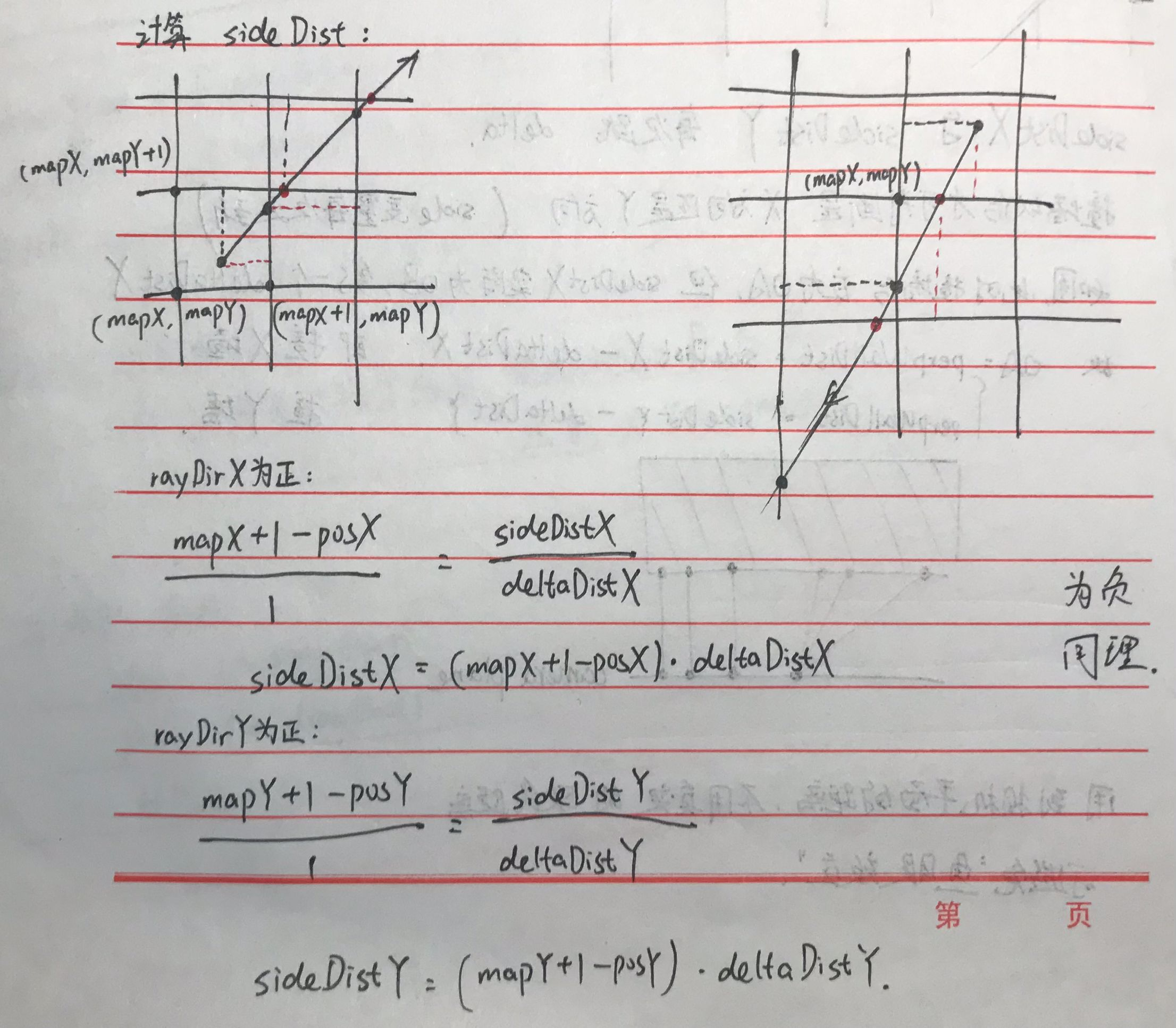
对应的代码如下:
1 | //calculate step and initial sideDist |
执行DDA算法
代码如下:
1 | //perform DDA |
这段代码还是挺简单的,可以在纸上画一画,就能理解过程了
可能等我有空了会做一个manim动画演示?应该会做吧
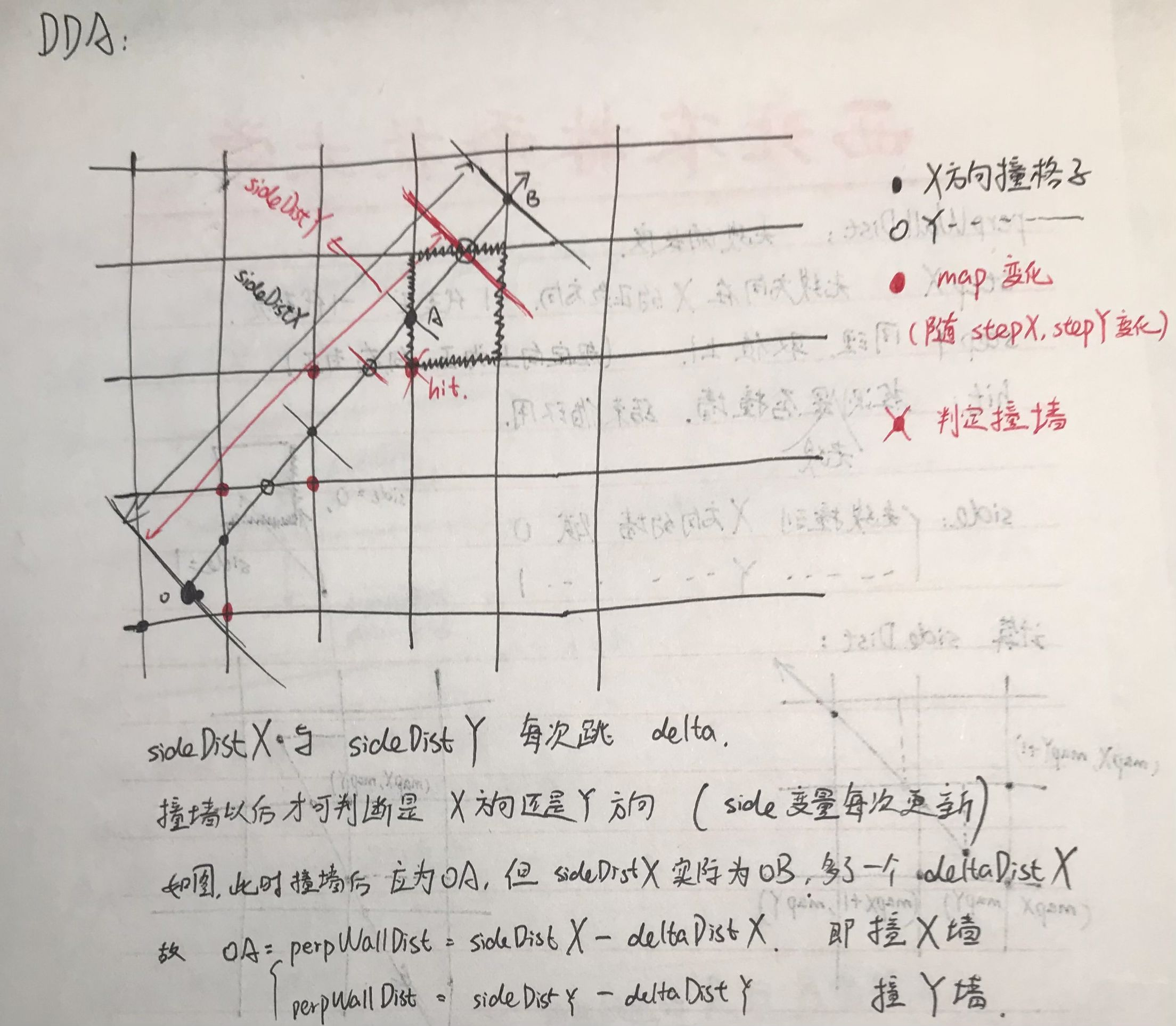
只需要注意,判断撞墙以后对应的长度会多加一个,于是需要减掉
计算对应墙的高度
当DDA结束以后,我们要计算光线的长度,这样才能求出对应墙的高度
注意:我们不用角色到墙壁实际的欧氏距离(即碰到墙后光线的长度),而是用相机平面到墙壁的距离来计算长度
如果用实际欧氏距离,就会出现“鱼眼效应”,如图所示:
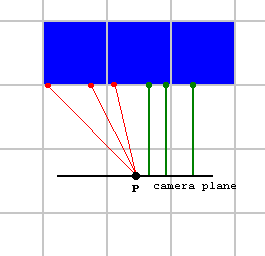
在玩家角色P的左边,显示了一些从墙的击中点到玩家的红色光线,代表欧几里得距离
在玩家的右边,显示了一些从墙的击中点直接到相机平面的绿色光线,而不是到玩家,这些绿线的长度是我们将使用的垂直距离的例子,而不是直接的欧几里得距离
在示例图中,玩家正在直接看着墙,而在这种情况下,我们期望墙的底部和顶部在屏幕上形成一条完美的水平线,即面朝着墙,希望墙高度相等,如图所示:

然而,红色的光线都有不同的长度,所以会为不同的垂直条纹计算出不同的墙高,从而产生圆润的效果
右边的绿色光线都有相同的长度,所以会给出正确的结果,当玩家旋转时仍然适用
用一个比较极端的例子来描述“用相机平面的距离代替欧拉距离”:
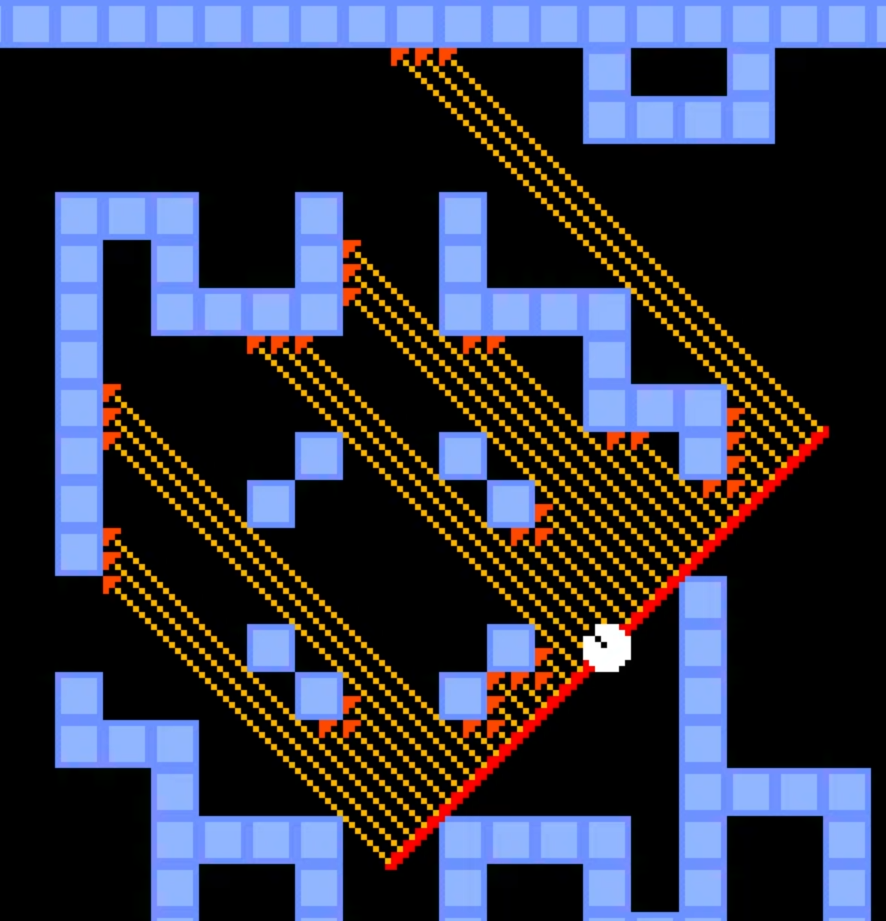
这样就可以很好地理解了,只不过这个例子画的太极端了,完全没有考虑视野范围的情况
正常来说是应该计算出FOV里对应所有光线的终点,再拿相机平面到这些点的距离算出墙的高度
参考原教程,里面给出了证明过程,证明了这样的计算就能避免鱼眼效应
1 | //教程里这部分解释的比较清楚了 |
详细的证明过程整理如下,以这个图为例:
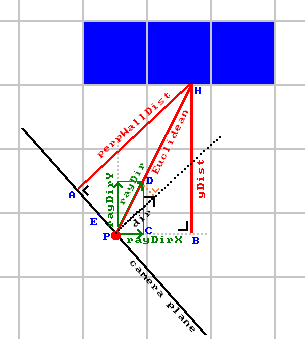
如果上文计算deltaDistX和deltaDistY的代码如下:
1 | // 鱼眼效应 |
就会产生“鱼眼效应”,如下图所示,如果不嫌晕的话,其实挺有意思的

不同墙选不同颜色
我们可以规定,如果光线撞到Y墙,就让颜色的RGB减半,视觉效果上就会更暗,这样会有更好的显示效果
1 | //choose wall color |
屏幕对应位置画线
先计算线对应的起点drawStart和终点drawEnd,再带入画线函数
计算过程如图:
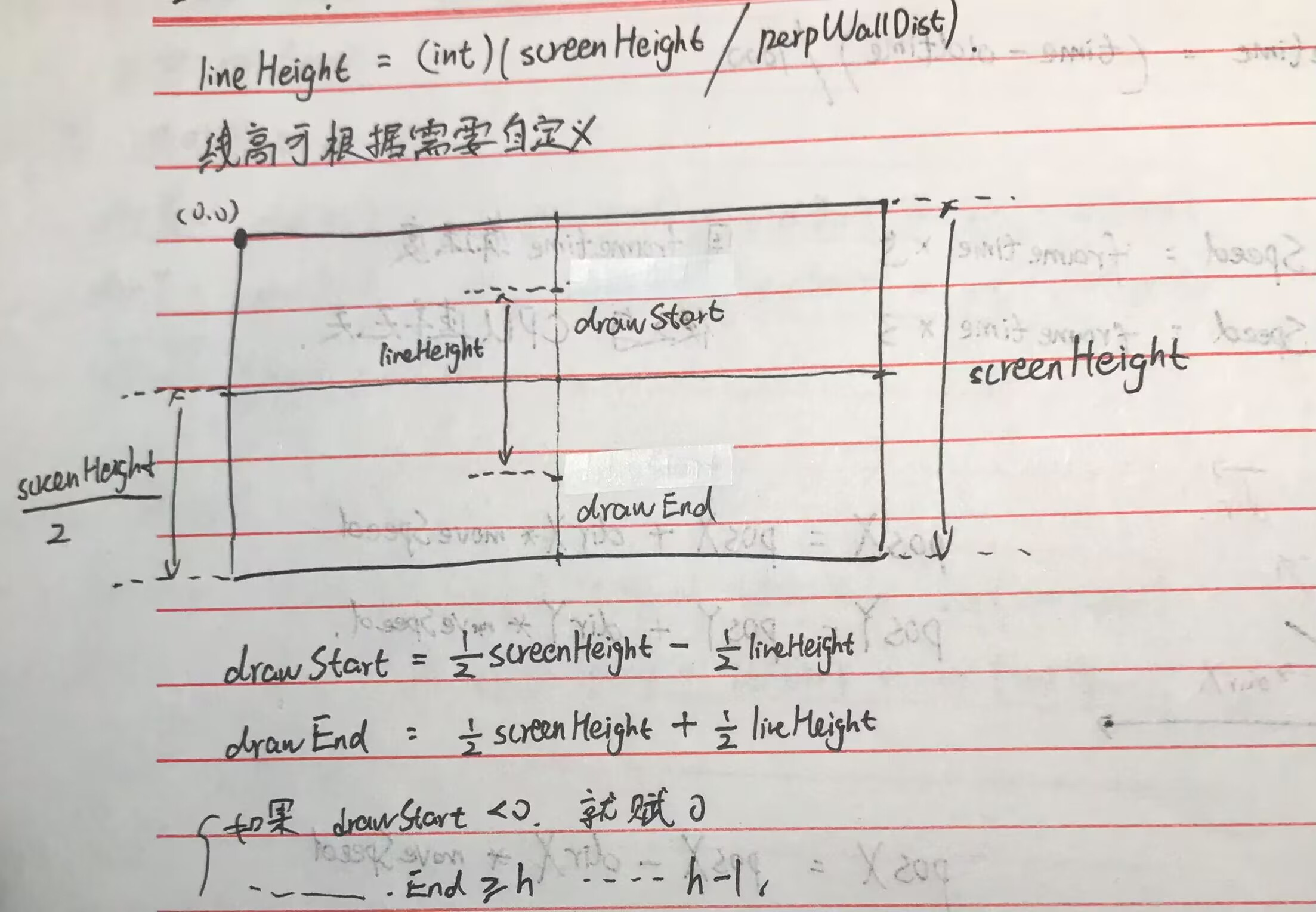
画线函数指定了屏幕对应的x坐标,线的起点和终点,还有对应的颜色
画线我单独写了一个函数:verLine,在DDA函数的最后直接调用就行
代码如下:
1 | //calculate lowest and highest pixel to fill in current stripe |
画线函数定义如下
1 | //画线 |
至此,DDA函数结束
人物移动逻辑
对应了main函数中的Move函数
具体实现涉及到方向矩阵的乘法,说白了就是二维矩阵乘法
先计算帧之间的时间,用于计算速度
1 | //timing for input and FPS counter |
其中getTicks函数定义如下:
1 | unsigned long getTicks() |
前后走
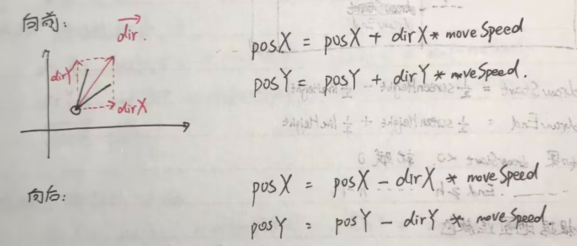
很好理解,对应坐标加上速度乘方向
对应代码如下:
1 | //move forward if no wall in front of you |
左右走
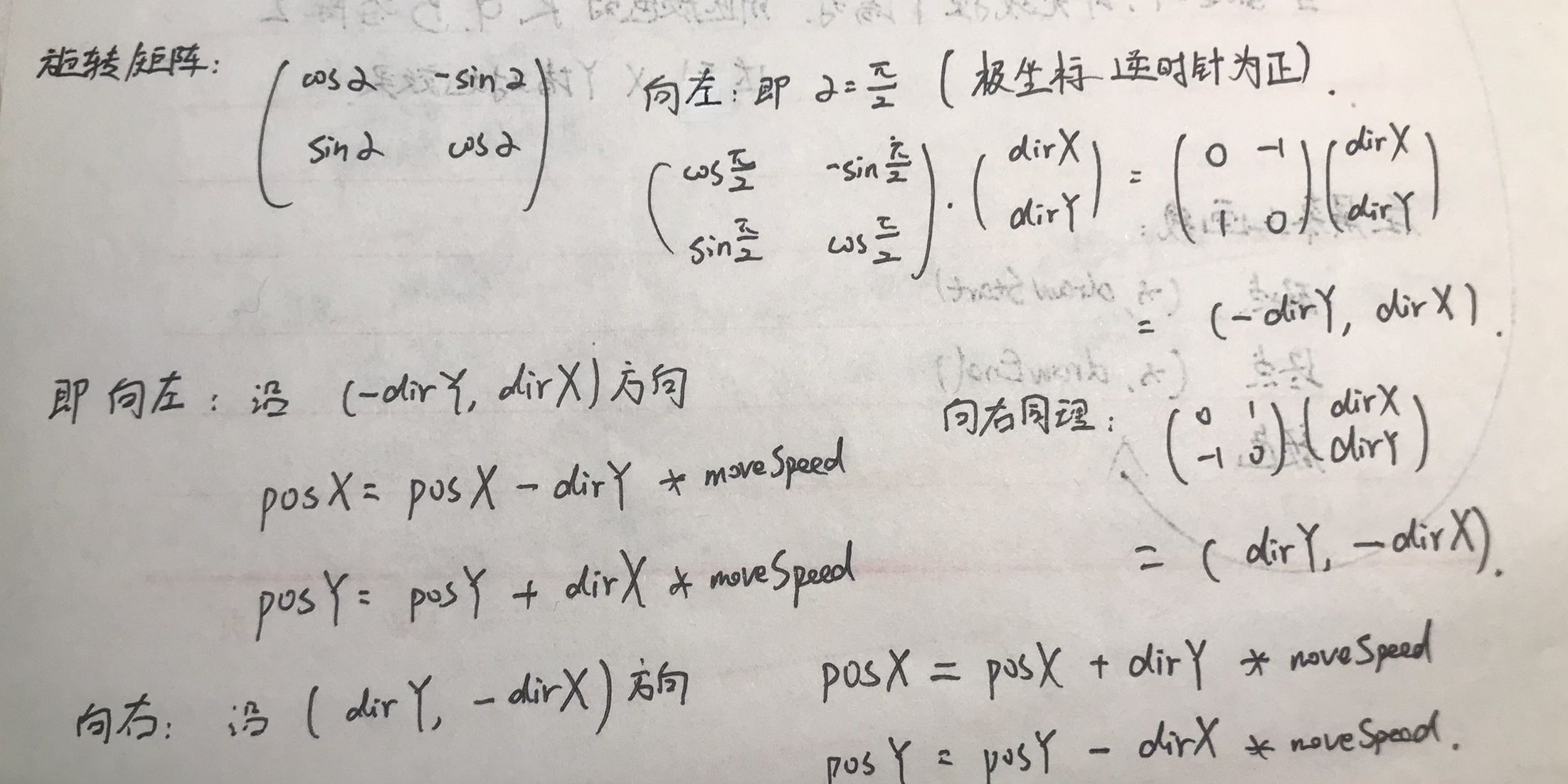
左右走也类似于前后走,只不过对应方向改变了
对应代码如下:
1 | //向右走,原理还是跟前后走一样,只是方向用矩阵相乘重新算了 |
视角左右转
注意:\(\overrightarrow{dir}\)和\(\overrightarrow{plane}\)两个向量同时都要旋转

对应代码如下:
1 | //rotate to the right |
至此,Move函数结束
最后的效果
源代码
无纹理,最基本Raycasting的实现,源代码如下
1 |
|
加纹理版
具体实现思路和最基础版本完全一样,只是略有不同
纹理部分会代替最基本实现中“颜色选择”部分
可在这里查看源代码
变量声明处多了与纹理相关的定义,顺便换一张地图,重新定义角色起始位置:
1 |
|
main函数多了读取纹理的操作,把对应的纹理读取到Texture texture[8]这个纹理数组中:
1 | int main() |
LoadTexture定义如下:
1 | void LoadTexture() |
原教程的纹理添加过程我也试过,但是非常卡,并且图像显示还有很大问题
于是这里只记录用SFML实现纹理的方法,具体参考为YouTube视频以及对应的代码
原作者英文口语还是很奇怪的,代码也是研究了很久才看明白,不过最后全变成我的东西了
纹理添加的代码具体更新内容,还是在DDA函数里修改:
1 | void DDA_algorithm(RenderWindow& window) |
计算纹理对应坐标texX
此处紧接着DDA算法结束
1 | //texturing calculations |
变量texNum是当前地图方块的值减1,原因是存在纹理0,但地图砖块0没有纹理,因为它代表一个空的空间
1 | //calculate value of wallX |
wallX表示墙被击中的确切位置,而不仅仅是墙的整数坐标
具体的计算方法,用到了相似三角形的内容,需要参考“避免鱼眼效应证明”那一块的内容
具体来说,计算墙被光线击中具体位置与玩家坐标之间差值Dist的公式如下:
\[
\begin{align*}
\frac{|\overrightarrow{\text{dir}}|=1}{\text{perpWallDist}}&=\frac{\text{rayDirY}}{\text{yDist}}=\frac{\text{rayDirX}}{\text{xDist}}\\\\
\text{即:}\text{yDist}&=\text{perpWallDist}\cdot \text{rayDirY}\\
\text{xDist}&=\text{perpWallDist}\cdot \text{rayDirX}\\
\end{align*}
\]
具体的差值xDist和yDist算出来以后,要根据方向选择是在玩家坐标的基础上加还是减,但是因为rayDirX和rayDirY本来就有正负号,因此刚好直接用,体现在代码里就是这段代码:
1 | double wallX; //where exactly the wall was hit |
这里用的floor函数,用于将一个数向下取整,即floor()函数会返回不大于输入参数的最大整数
在C++中,将一个浮点数转换为整数(即
(int)wallX)时,会直接舍去小数部分。例如,(int)3.14的结果是3,(int)-3.14的结果是-3。而
floor()函数则会返回不大于输入参数的最大整数。例如,floor(3.14)的结果是3,floor(-3.14)的结果是-4。所以,如果
wallX是正数,那么wallX -= floor(wallX);和wallX -= (int)wallX;的结果是一样的。但是,如果wallX是负数,那么这两种操作的结果就会不同。
wallX -= floor((wallX))会只保留小数部分,取值范围就在\([0,1)\)
1 | //x coordinate on the texture |
texX是纹理的x坐标,根据wallX计算出来的,是光线撞到墙,墙的位置对应到纹理上的x坐标,即用wallX算出来的小数乘以texWidth,可以得到纹理上确切的x坐标
镜像处理
默认texX是纹理图像从左向右的x坐标
但是有两种情况计算出来的结果是从右向左的,会导致镜像翻转

如果不进行镜像处理,就会出现这样的情况:
这两个面看过去,鹰的头向左偏

从这两个面看过去,鹰的头向右偏

而原图的鹰头就是偏向右的

因此需要进行镜像处理
1 | // 防止镜像 |
纹理的Sprite
这部分的具体思路就与原教程不一样了
我的思路还是与画线一样,即画出纹理对应的一条线,宽为1像素,长为对应线的长度,只是颜色是直接拿纹理的颜色
具体实现,就是创建长为texHeight,宽为1像素的Sprite,对其设置对应纹理
1 | //为了获取纹理具体某一个坐标的像素颜色 |
再指定左上角位置为(x, round(0.5f * screenHeight - 0.5f * lineHeight)
至于Y起点指定的位置,为什么不是刚刚画线时的drawStart,我在后面会详细解释这个问题,还是挺有意思的一个小bug
1 | //设置sprite的位置,坐标指定了左上角的位置 |
长度值是texHeight,而我们应该画线的长度是lineHeight,所以对这个Sprite进行缩放
1 | //设置sprite的缩放因子 |
最后还是和之前一样的思路,Y墙上的颜色要变暗,就进行处理
SFML纹理颜色的处理需要用“调制混合”的概念
举个例子:原来的R通道为200,与128混合为:200 * 128 / 255 = 100,实现了颜色除以2的效果
1 | //利用SFML中sprite的setColor功能,使y墙变暗 |
绘制纹理Sprite
这个就简单了,因为纹理Sprite我们已经设置位置和大小,直接画出来就行了
1 | // 绘制sprite |
最后的效果

源代码
带纹理Raycasting的实现,源代码如下
1 |
|
加点东西
本来是准备结束的,但是在实际演示的前一天,在我给同学展示的时候,有个同学就提出来了:这样看不出地图会迷路,是不是加个小地图会更好?
我一想,太对了,当天直接完成了小地图的部分
我再一想,既然小地图都做了,为什么不把角色视野范围做出了?
太对了,当天直接熬夜完成了视野范围的部分
本来想给地板和天花板都上个纹理的,但是因为实际做了之后帧数特别低,甚至无法跑到60帧,就搁置了,以后有时间再进行优化,最后就是只给地板和天花板弄了个纯色
新的main函数
1 | int main() |
加了对应画天花板地板的函数DrawFloorCeiling和画小地图的函数drawMiniMap
其中,按Tab键可以开关小地图,实际上加一个标志位,每次按键检测设置flag即可,很容易
加地板天花板
这个还是很容易的,只需要显示两个有色矩形,一个为天花板,一个为地板
在DDA画线之前画上天花板和地板就行了
1 | void DrawFloorCeiling(RenderWindow& window) |
加小地图和视野范围
这个还是挺有趣的
先在全局变量添加小地图参数和FOV视野变量
1 | //创建一个表示视野范围的三角扇形 |
如果把角色相关的东西都定义在一个类里,修改就不会很头疼了
但是因为这些代码是在原来基础上添加的,就不想重新构建了
1 | //要注意:SFML中的y轴是向下的,而用二维数组计算时y轴是向上的 |
对应扇形参数的设置我添加到DDA算法中了:
1 | void DDA_algorithm(RenderWindow& window) |
其他内容都没修改
最后的效果

源代码
带纹理,画天花板地板,画小地图FOV视野Raycasting的实现,源代码如下
1 |
|
展示的Demonstration
展示的逻辑
就是用按键控制一系列显示,我感觉当时展示还挺成功的
唯一的遗憾是没有实时演示这个程序,而是录的视频,因为教室的电脑没装VisualStudio的运行环境
具体演示过程如下:
先只显示小地图,角色可以在小地图上自由行走,为了突出展示的主题“给二维数组一点小小的伪3D震撼”
再显示人物视野范围,按Shift开启
再缩小小地图,按<键或减号键缩小
再显示伪3D效果,按回车开启
再显示地板天花板,按B开启
再显示纹理,按T开启
按照这个顺序演示,确实感觉太牛逼了,层层递进,一波一波的震撼,尤其是逐渐缩小小地图,按回车无缝衔接,显示Raycasting的结果,真正做到了给二维数组一点小小的伪3D震撼
对应修改
添加对应的Flag标志:
1 | //是否画伪3D效果 回车键 |
main函数修改如下:
1 | int main() |
这里实际上还涉及到SFML的一个小问题:按键检测
在移动逻辑中,我们用的逻辑是sf::Keyboard::isKeyPressed(sf::Keyboard::W)
而在改变flag时,我们用的逻辑是event事件的sf::Event::KeyPressed
具体为:
1 | //sf::Keyboard::isKeyPressed函数会在每一帧都检测键盘的状态 |
原因如下:
sf::Keyboard::isKeyPressed函数会在每一帧都检测键盘的状态
sf::Event::KeyPressed事件只会在按键被按下的那一帧触发一次,即使你按住按键不放,它也不会在下一帧再次触发
因此,使用sf::Event::KeyPressed事件可以确保Flag的值只会被反转一次
源代码
1 |
|
遇到的问题
纹理问题
我在编码过程中碰到了如图所示的问题

开什么玩笑?要吐了!
那么这是怎么会是呢?
为什么会出现“墙往两侧倒”的这种情况?
为什么刚刚纯色版本没出现这个问题?
其实很简单,因为纯色版本也有这样的问题,只是纯色没有纹理,看不出来这样的效果
最主要的问题就出在“设置线的起点”这条语句上
先看看纯色的这里是怎么做的:
1 | int drawStart = -lineHeight / 2 + screenHeight / 2; |
我们在设置起点的时候,明确指定了:如果起点小于0,就把drawStart强行赋值为0
再来看看纹理设置位置:
1 | //设置sprite的位置,坐标指定了左上角的位置 |
这就导致了问题:当这个墙超过视野范围,计算的起点必须是负数,但是强行赋值为0,就会导致纹理的起点变成0
在原教程中,把起点强行设置为0,可能是因为原教程里用的图形库不支持负数坐标,并且显示逻辑也跟我在SFML中用的不一样
但是在SFML中是支持坐标超出屏幕范围的,也就是支持坐标指定为负数,那就不用担心了
我们就把设置位置这条的Y坐标起始位置修改为drawStart的计算过程:
1 | //设置sprite的位置,坐标指定了左上角的位置 |
这样就解决问题了
经过这个bug,深刻认识到参考只能是参考,和实际一定会有差别,代码不能直接复制粘贴啊,笑拉了
参考资料
First-person shooter - Wikipedia
Making my First RAYCASTING Game in C++
Kofybrek/Raycasting: Tried to write a ray casting game with no experience
