Python问题

令人感叹，虽然有C++和Java的编程基础，但是Python没有系统地学过，所以很多常用的，好用的库最基本的东西都不会，于是在此记录

可能都是一些最基本的问题，但是我确实不会，不得不碰到一个记录一个

我觉得真得系统地学习一门编程语言，因为这门语言可能会有一些你没接触过的新语法，你没见过的牛逼库

pandas库记录

这个库总体上是用于数据分析的，可以用于读取csv文件

常用的数据结构：Series和DataFrame

Series

pandas.Series( data, index, dtype, name, copy)

Pandas Series 类似表格中的一个列，类似于一维数组，带有可以自定义的索引（类似于C++里的键值对，索引是键，元素是值）

在不指定索引的情况下，索引就从0开始，类似于数组的下标

也可以指定索引，如：

import pandas as pd

a = ["Google", "Runoob", "Wiki"]

#自定义索引
myvar = pd.Series(a, index = ["x", "y", "z"])

print(myvar)		
print(myvar["y"])	#根据索引打印值

----------------------------------------------------

输出为：
x    Google
y    Runoob
z      Wiki
dtype: object
Runoob

索引对齐问题

先来看我机器学习求岭回归时中出现的一个问题：

# 计算岭回归系数
Beta = np.linalg.inv(x_scaled.T @ x_scaled + lambda_i * np.eye(x_scaled.shape[1])) @ x_scaled.T @ y
print("Beta:\n\n",Beta,'\n')
print("x_std:\n\n",x_std,'\n')

# 还原为原自变量的系数
Beta_Final = Beta / x_std
Beta_Final_0 = np.mean(y) - np.sum(Beta * x_mean / x_std)
print("Beta_Final:\n\n",Beta_Final)

输出结果如下：

Beta:

 0   -0.322031
1   -0.092444 
2    1.178097
3    0.469515
4    4.291294
5   -4.388335
6   -1.076790
7    1.262912
dtype: float64

x_std:

 Sex               0.827716
Length            0.120079
Diameter          0.099228
Height            0.041822
Whole weight      0.490330
Shucked weight    0.221936
Viscera weight    0.109601
Shell weight      0.139186
dtype: float64

Beta_Final:

 0                NaN
1                NaN
2                NaN
3                NaN
4                NaN
5                NaN
6                NaN
7                NaN
Diameter         NaN
Height           NaN
Length           NaN
Sex              NaN
Shell weight     NaN
Shucked weight   NaN
Viscera weight   NaN
Whole weight     NaN
dtype: float64

我在这里想实现的操作是Beta_Final = Beta / x_std = Beta / x_std，即把Beta的每一项与x_std的每一项做除法，然后存在Beta_Final中。这两个向量都是8x1的，所以绝对可以计算

但是结果输出的Beta_Final却不是我想要的结果：可以看到每一项都是NaN，且维数变成了16x1，怎么会是呢？

我去问了bing：

我注意到你的x_std的索引是你的特征名（‘Sex’，‘Length’，'Diameter’等），而你的Beta的索引是数字（0到7）。这就是为什么你在计算Beta_Final时得到了全是NaN的结果。

为了解决这个问题，你需要确保在计算之前，你的Beta和x_std有相同的索引。你可以在计算Beta_Final之前，使用以下代码来更新Beta的索引：
1
>Beta.index = x_std.index
然后再计算 Beta_Final = Beta / x_std, 这样应该就可以得到正确的结果了。

在Pandas中，当对两个Series对象进行操作时，Pandas会尝试对齐它们的索引。如果在一个Series中找不到对应的索引，那么结果就会被设置为NaN。这就是为什么你在计算Beta_Final = Beta / x_std时得到了全是NaN的结果，因为Beta和x_std的索引不匹配。

这种行为是Pandas的设计决策之一，目的是为了处理实际数据分析中常见的问题，比如数据缺失、数据顺序不一致等等。当然，这也意味着我们在使用Pandas进行计算时，需要注意保持索引的一致性。

如果你想要按照位置（而不是按照索引）来进行计算，你可以使用Numpy数组来代替Pandas Series。Numpy数组没有索引，所以它们之间的操作都是基于位置的。例如，你可以这样计算Beta_Final：
1
>Beta_Final = Beta.values / x_std.values
这里，.values属性会返回一个Numpy数组，包含了Series中的值。

太详细了，给出的解决方案太可行了，真得给bing磕大头吧

元素级别的乘法

我现在想实现对一个样本每一维的元素和Beta_Final的每一个元素进行乘法：

有一个4177x8的Dataframe: x，一个8x1的Series: Beta_Final，想要对x的每一行和Beta_Final进行对应元素的乘法运算。具体来说，就是x的第一行的第一个元素乘以Beta_Final的第一个元素，x的第一行的第二个元素乘以Beta_Final的第二个元素，以此类推

用x * Beta_Final就可以实现

DataFrame

pandas.DataFrame( data, index, columns, dtype, copy)

DataFrame 是一个表格型的数据结构，它含有一组有序的列，每列可以是不同的值类型（数值、字符串、布尔型值）

DataFrame 既有行索引也有列索引，它可以被看做由 Series 组成的字典（共同用一个索引）

矩阵乘法

DataFrame可以直接与numpy二维数组做矩阵乘法：

import pandas as pd
import numpy as np

# 创建一个DataFrame
df = pd.DataFrame(np.random.rand(3, 2), columns=['a', 'b'])

# 创建一个numpy数组
arr = np.array([[1, 2, 3], [4, 5, 6]])

# 使用@运算符进行矩阵乘法
result_at = df @ arr

# 使用dot方法进行矩阵乘法
result_dot = df.dot(arr)

df是一个3x2的DataFrame，arr是一个2x3的numpy数组

使用@运算符，我们可以得到一个3x3的结果DataFrame

使用dot方法，我们可以得到一个3x3的结果DataFrame

numpy库记录

生成序列

生成序列可以用到numpy的两个函数：

np.linspace和np.arange

np.arange(start, stop, step)：这个函数会生成一个从start开始，到stop结束（但不包含stop），步长为step的数列

例如，np.arange(0, 10, 1)会生成一个从0开始，到10结束（但不包含10），步长为1的数列：[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

np.linspace(start, stop, num)：这个函数会生成一个从start开始，到stop结束（默认包含stop），总共有num个元素的数列

例如，np.linspace(0, 10, 11)会生成一个从0开始，到10结束（包含10），总共有11个元素的数列：[0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]

总结一下，主要的区别在于：

np.arange()是按照指定的步长来生成数列，而且不包含结束值

np.linspace()是按照指定的元素个数来生成数列，而且默认包含结束值

`axis`

axis可以指定对一个二维数组进行指定方向的操作，即可以按行方向(axis=1)，也可以按列方向(axis=0)

例子如下

import numpy as np

arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr)

print(np.sum(arr, axis=0))

print(np.sum(arr, axis=1))

得到的输出如下：

# print(arr)的输出
[[1 2 3]
 [4 5 6]]

# print(np.sum(arr, axis=0))的输出
[5 7 9]

# print(np.sum(arr, axis=1))的输出
[ 6 15]

可见，在求和函数中指定axis=0是对每一列求和，axis=1是对每一行求和

找最小值和对应的下标

比如找一个岭参数使误差最小，我建立了一个岭参数数组lambdaList = np.arange(1, 10.1, 0.1)，再遍历其中每一个元素计算一个对应的误差存入数组Errors = []中，我要找到最小的误差以及对应的下标，这样就能得知对应的岭参数了

其他语言里写一个循环就能实现，但是这里是Python，要会用轮子：np.argmin()和np.min()

1
2
3

print(np.min(Errors))			#找到Errors最小值
index_min = np.argmin(Errors)	#找到Errors最小值对应的下标
print(lambdaList[index_min])

同理，还有max和argmax函数

`np.zeros()`生成指定数组

numpy.zeros函数用于创建指定形状和数据类型的数组，该数组填充为零。以下是其基本用法：
1
>numpy.zeros(shape, dtype=float, order='C')
参数说明：

shape：整数或整数的元组。新数组的形状，例如(2, 3)或2。

dtype：数据类型，可选。期望的数组数据类型，例如numpy.int8。默认是numpy.float64。

order：'C'或'F'，可选，默认为'C'。是否以行主（C风格）或列主（Fortran风格）顺序在内存中存储多维数据。

返回值：

返回一个填充有零的具有给定形状、数据类型和顺序的数组。

示例：
1
2
3
4
5
6
7
8
9
10
>import numpy as np

># 创建一个长度为5的零向量
>print(np.zeros(5))

># 创建一个2x2的零矩阵
>print(np.zeros((2, 2)))

># 创建一个自定义数据类型的零数组
>print(np.zeros((2,), dtype=[('x', 'i4'), ('y', 'i4')]))

我现在需要一个二维矩阵，我已知了行数和列数，可以用numpy来产生一个矩阵

1 2	#生成A矩阵：num行degree+1列 Mat_A = np.zeros((num, degree+1))

注意这里的参数是有两个括号：

在NumPy的np.zeros()函数中，我们需要使用两个括号，是因为这个函数的参数shape需要一个元组来表示数组的形状。元组是Python中的一种数据类型，用于存储一组有序的元素。元组是不可变的，也就是说，一旦创建了元组，就不能更改它的内容。

在np.zeros()函数中，如果我们想创建一个二维数组，我们需要提供一个包含两个元素的元组，其中第一个元素表示行数，第二个元素表示列数。例如，np.zeros((3, 4))会创建一个3行4列的二维数组。

所以，当我们写np.zeros((3, 4))时，外面的一对括号是函数调用的括号，里面的一对括号则是创建元组的括号。

矩阵相关

如我求岭参数用到的运算：

1	Beta = np.linalg.inv(x_scaled.T @ x_scaled + lambda_i * np.eye(x_scaled.shape[1])) @ x_scaled.T @ y

逆矩阵

np.linalg.inv()为求逆运算

如果矩阵是numpy.matrix类型，可以使用.I属性来求逆矩阵，如：

# 定义一个可逆矩阵
A = np.matrix([[1, 2], [3, 4]])

# 计算矩阵的逆
A_inv = A.I

转置矩阵

x_scaled.T是求x_scaled的转置矩阵

也可以用np.transpose(x_scaled)实现

矩阵乘法

@是求矩阵乘积

也可以用np.dot()函数实现

np.dot()函数：

np.dot 是 numpy 库中的一个函数，主要用于矩阵的乘法运算，包括：向量内积、多维矩阵乘法、矩阵与向量的乘法。

向量内积：向量是一维矩阵，两个向量进行内积运算时，需要保证两个向量包含的元素个数是相同的。
1
2
3
4
5
>import numpy as np
>x = np.array([1,2,3,4,5,6,7])
>y = np.array([2,3,4,5,6,7,8])
>result = np.dot(x, y)
>print(result)  # 输出结果：168
多维矩阵乘法：两个矩阵（x,y）如果可以进行乘法运算，需要满足以下条件：x为mxn阶矩阵，y为nxp阶矩阵，则相乘的结果result为mxp阶矩阵。
1
2
3
4
5
>import numpy as np
>x = np.array([[1,2,3], [4,5,6]])
>y = np.array([[2,3], [4,5], [6,7]])
>result = np.dot(x, y)
>print(result)  # 输出结果：[[28 34] [64 79]]
矩阵与向量乘法：矩阵x为mxn阶，向量y为n阶向量，则矩阵x和向量y可以进行乘法运算，结果为m阶向量。
1
2
3
4
5
>import numpy as np
>x = np.array([[1,2,3], [4,5,6]])
>y = np.array([1,2,3])
>result = np.dot(x, y)
>print(result)  # 输出结果：[14 32]

获取矩阵行列信息

x_scaled.shape[1]是获取x_scaled的列数

同理，x_scaled.shape[0]是获取行数

`reshape()`函数

y = np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
]).reshape(20, 1)

reshape(20, 1) 将 y这个一维数组转换成了一个二维数组，其中 20 是行数，1 是列数。

具体来说，y 原本是一个包含20个元素的一维数组：
1
2
3
4
>y = np.array([
   3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
   11, 13, 13, 16, 17, 18, 17, 19, 21
>])
通过 reshape(20, 1)，y 被转换成了一个二维数组，有 20 行和 1 列。
1
2
3
4
>y = np.array([
   [3], [4], [5], [5], [2], [4], [7], [8], [11], [8],
   [12], [11], [13], [13], [16], [17], [18], [17], [19], [21]
>])
reshape 函数在使用时有一些限制。它要求每个维度的乘积必须等于原来的元素个数。也就是说，不能随意地改变数组的形状，必须保证改变后的形状与原始形状的元素总数相同。

例如，如果你有一个包含12个元素的一维数组，你可以将其重塑为形状为(3, 4)或(2, 6)的二维数组，因为这些形状的元素总数仍然是12。但是，你不能将其重塑为形状为(5, 5)的数组，因为这需要25个元素，而原始数组只有12个元素。

此外，reshape 函数允许使用-1 作为形状的一个维度。在这种情况下，-1 所在的维度的大小将根据数组的长度和其他维度的大小自动计算。例如，如果你有一个包含12个元素的一维数组，你可以使用 reshape(-1, 4) 来将其重塑为一个有4列的二维数组，行数会根据元素总数自动计算。

也就是说，np.reshape函数可以改变一个数组的形状，但是它不能增加数组的元素数量

numpy特有的下标访问方法

在Python的正常语法中，访问一个二维数组的元素与C++类似：

Mat[i][j]，指定行列下标的方式

但是在numpy中（即用numpy创建的二维数组），可以用Mat[i, j]的语法来访问第i行第j列的元素；这种方法称为“多维索引”

特殊下标

-1这个下标可以表示最后一个元素（这个下标不止在numpy库中可以用，Python的列表也可以用，只是在numpy使用过程中遇见了，记录在此）

例如：

# 创建一个列表
list = [1, 2, 3, 4, 5]

# 输出列表的最后一个元素
print(list[-1])  # 输出：5

# 创建一个字符串
str = 'Hello, world!'

# 输出字符串的最后一个字符
print(str[-1])  # 输出：!

还可以使用:表示一整行或一整列，这个叫“切片功能”，具体介绍如下

`:`切片功能

例如：

Temp[:, i]里的:表示选中全部行，表示了Temp的第i列

Temp[i, :]里的:表示选中全部列，表示了Temp的第i行

比如编写克莱姆法则求解方程时就用到了这个，可以直接替换其中一列：

#A为方阵，b为n维向量
def MyCramer(A, b):
    n = len(A)
    if np.linalg.det(A) == 0:
        return "矩阵A的行列式为0，无法使用克莱姆法则求解。"
    else:
        x = np.zeros(n)
        for i in range(n):
            Temp = A.copy()
            # 将第i列换为b
            Temp[:, i] = b
            x[i] = np.linalg.det(Temp) / np.linalg.det(A)
        return x

再比如我有个矩阵A，一个n维向量b，我现在要创建一个关于A, b的增广矩阵：

#创建增广矩阵
Augmented_Mat = np.zeros((A.shape[0], A.shape[1] + 1))
#把A复制到增广矩阵的前n列
Augmented_Mat[:, :A.shape[1]] = A
#把b复制到增广矩阵最后一列
Augmented_Mat[:, A.shape[1]] = b
#最后一列也可以用-1这个下标来指明，如 Augmented_Mat[:, -1] = b

切片功能的详细解释：

在numpy中，:操作符可以用来选择数组的一部分，这被称为切片（slicing）。在二维数组中，你可以使用两个:操作符来分别选择行和列。

切片的基本语法是[start:stop:step]：

start：开始索引，即切片的起始位置。如果我们省略start，则切片从第一个元素开始。

stop：结束索引，即切片的结束位置。需要注意的是，结束索引是不包含在切片内的。如果我们省略stop，则切片一直到数组的最后一个元素。

step：步长，即切片中每两个元素之间的间隔。如果我们省略step，则默认步长为1。

例如，arr[1:5]表示从索引1开始到索引5（不包含）的元素，arr[0:8:2]表示从索引0开始到索引8（不包含），步长为2的元素，arr[3:]表示从索引3开始到最后的所有元素，arr[:]表示数组的所有元素。

在二维数组中，你可以使用逗号,来分隔行和列的切片。例如，arr[1:3, 2:4]表示选择第1行到第2行（不包含第3行），第2列到第3列（不包含第4列）的元素。

在之前的代码Augmented_Mat[:, :A.shape[1]] = A中，:表示选择所有行，:A.shape[1]表示选择从第一列到第n列（即下标从0到A.shape[1] - 1，即前n列，不包括下标为A.shape[1]的列）。A.shape[1]是矩阵A的列数。所以，Augmented_Mat[:, :A.shape[1]]表示的是增广矩阵的前n列。

引用赋值

我在列主元高斯消元法的实现时碰到了这样一个问题：

我现在需要交换矩阵的两行，我这样写：

#交换最大行和当前行（把主元放在对角线上）
#因为是方阵，所以col = row，此处用col当做row，属于变量名没起好
Temprow = Augmented_Mat[col,:]
Augmented_Mat[col,:] = Augmented_Mat[maxRow_index,:]
Augmented_Mat[maxRow_index,:] = Temprow

很常规的想法对吧，跟C++里交换两个变量一样，拿个Temp存储即可

但是出问题了：我尝试输出每一次换行后的增广矩阵，输出结果出现了这样：

[[429. 137. 398. 440. 382. -16.]
 [403. 279.  77. 204. 152. 319.]
 [209.  93. 249. 241.   7.  -7.]
 [139. 488. 390. 245. 194.  52.]
 [-73. -71. 345. 349. 471. -34.]]

[[ 429.          137.          398.          440.          382.
   -16.        ]
 [   0.          443.61072261  261.04428904  102.43589744   70.22843823
    57.18414918]
 [   0.           26.25641026   55.1025641    26.64102564 -179.1025641
     0.79487179]
 [   0.          443.61072261  261.04428904  102.43589744   70.22843823
    57.18414918]
 [   0.          -47.68764569  412.72494172  423.87179487  536.002331
   -36.72261072]]

[[429.         137.         398.         440.         382.
  -16.        ]
 [  0.         443.61072261 261.04428904 102.43589744  70.22843823
   57.18414918]
 [  0.           0.         440.78690446 434.88353677 543.55180785
  -30.57538004]
 [  0.           0.           0.           0.           0.
    0.        ]
 [  0.           0.         440.78690446 434.88353677 543.55180785
  -30.57538004]]

[[429.         137.         398.         440.         382.
  -16.        ]
 [  0.         443.61072261 261.04428904 102.43589744  70.22843823
   57.18414918]
 [  0.           0.         440.78690446 434.88353677 543.55180785
  -30.57538004]
 [  0.           0.           0.           0.           0.
    0.        ]
 [  0.           0.           0.           0.           0.
    0.        ]]

E:\Code\The First Term of Junior\数值分析\第七次作业\Calculate.py:81: RuntimeWarning: invalid value encountered in double_scalars
  k = Augmented_Mat[row][col] / Augmented_Mat[col][col]
[[429.         137.         398.         440.         382.
  -16.        ]
 [  0.         443.61072261 261.04428904 102.43589744  70.22843823
   57.18414918]
 [  0.           0.         440.78690446 434.88353677 543.55180785
  -30.57538004]
 [  0.           0.           0.           0.           0.
    0.        ]
 [  0.           0.           0.           0.                  nan
           nan]]

竟然出现了全是0的几行，不可能啊？

就算会出现线性相关的两行，那概率应该是很低的，毕竟我生成随机数是从-100到500，运行了好几次都是这样的结果

于是我就把这段代码扔给bing，果然还是我对Python理解不够的问题：

可能的原因是你的代码在进行行交换时可能出现了问题。在你的代码中，你使用了一个临时变量Temprow来存储一行的值，然后交换两行。但是，你需要注意的是，在numpy中，当你把一行赋值给一个变量时，这个变量实际上是指向那一行的一个引用，而不是那一行的一个副本。所以，当你修改这个变量的值时，原始矩阵的那一行的值也会被修改。

在Python中，当你把一个对象（比如一个列表或者一个numpy数组的一行）赋值给一个变量时，这个变量实际上是指向那个对象的一个引用，而不是那个对象的一个副本。这意味着，如果你修改这个变量的值，原始对象的值也会被修改。

让我们通过一个简单的例子来理解这个概念：
1
2
3
4
5
6
7
8
9
10
11
12
13
>import numpy as np

># 创建一个二维数组
>A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

># 把A的第一行赋值给row
>row = A[0, :]

># 修改row的值
>row[0] = 10

># 打印A
>print(A)
这段代码会输出：
1
2
3
>[[10  2  3]
[ 4  5  6]
[ 7  8  9]]
你可以看到，尽管我们只修改了row的值，但是A的值也被修改了。这是因为row是A第一行的一个引用，而不是一个副本。

所以，在你的代码中，当你写Temprow = Augmented_Mat[col,:]时，Temprow实际上是Augmented_Mat[col,:]这一行的一个引用。然后，当你写Augmented_Mat[col,:] = Augmented_Mat[maxRow_index,:]时，Augmented_Mat[col,:]这一行的值被修改了，Temprow的值也会跟着改变，因为它是Augmented_Mat[col,:]这一行的一个引用。

为了避免这个问题，你可以使用copy函数来创建一个行的副本，然后进行交换。例如，你可以这样写：
1
2
3
4
>#交换最大行和当前行（把主元放在对角线上）
>Temprow = Augmented_Mat[col,:].copy()
>Augmented_Mat[col,:] = Augmented_Mat[maxRow_index,:]
>Augmented_Mat[maxRow_index,:] = Temprow
这样，Temprow就是那一行的一个副本，而不是一个引用，你就可以安全地进行行交换了。

概括来说，我因为没能了解到“对象赋值是传递引用”这个细节而导致了出现两行完全一样的结果，于是一减就成一行全0了

好在numpy的数组都有.copy()方法，可以直接创建一个副本，就直接解决问题了

matplotlib.pyplot库记录

重置一张图片

plt.cla()：这个函数可以清除当前的图形。

plt.clf()：这个函数可以清除当前的图形，并删除所有的子图。

plt.figure()：这个函数会创建一个新的图形。如果在绘制新图形之前调用这个函数，那么新图形将会在一个新的空白图形上绘制。

用来正常显示负号和中文

1 2	plt.rcParams['font.sans-serif'] = ['SimHei'] # SimHei是一种支持中文的字体 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号

指定坐标轴

1
2
3

# 设置x轴和y轴的图例
plt.xlabel('X Axis')
plt.ylabel('Y Axis')

保存图片

保存图片用到plt.savefig()函数

注意plt.savefig()函数要用在plt.show()前，否则不能正常保存

例如

#画图
plt.plot(Runge_X, Runge_Y, label='龙格函数')
plt.plot(Piece_linear_X, Piece_linear_Y, label='分段线性插值', marker='o')
plt.plot(Hermite_X, Hermite_Y, label='两点三次埃尔米特插值', linestyle='--')
plt.legend()
plt.savefig('Runge.png')
plt.show()

感觉不如查看图的时候点左下角的保存

sympy库记录

符号计算库真是太好用了，点名感谢如何用一行代码打败修炼三十年的高数老师 [南京大学 IT 侠 iTalk]这个视频，带给我符号计算的启蒙

`subs()`函数替换

sympy中，可以用变量来代换符号变量，用到subs()函数，从而可以求值

subs()的替换规则如下：

符号表达式.subs(待替换的变量，替换的值)

如f.subs(x,2)

import sympy as sp

# 定义一个符号
x = sp.symbols('x')

# 定义一个符号表达式
f = x**2 + 2*x + 1

# 使用subs函数替换x的值
print(f.subs(x, 2))  # 输出：9

# 你也可以一次替换多个值
g = sp.sin(x) + sp.cos(x)
print(g.subs({sp.sin(x): 1, sp.cos(x): 0}))  # 输出：1

# 甚至可以替换符号
h = x**2
print(h.subs(x, y))  # 输出：y**2

例如我想给一个数组X里每一个值代入符号式中，我可以写一个循环遍历这个数组，也可以直接代换：

# 创建一个numpy数组
X = np.linspace(-1,1,11)

# 将result中的x替换为X中的值
result_subs = [result.subs(x, val) for val in X]

在这个例子中，result.subs(x, val)会将result中的x替换为val，然后[result.subs(x, val) for val in X]会为X中的每个值执行这个替换操作，从而得到一个新的列表result_subs

也算是记录了Python的特殊写法吧

`integrate()`积分

sympy的积分可以用integrate计算：

sp.integrate(符号表达式，对谁积分(也可带范围表示定积分))

如：sp.integrate(f, x)为不定积分，sp.integrate(f, (x, 0, 1))为定积分

import sympy as sp

x = sp.symbols('x')

# 计算不定积分∫x dx
f = sp.integrate(x, x)	#对x里的x积分，第一个为被积的符号表达式，第二个参数为对谁积分
print(f)  # 输出：x**2/2

# 计算定积分∫_0^1 x dx
f = sp.integrate(x, (x, 0, 1))
print(f)  # 输出：1/2

# 定义一个符号表达式
f = x**2 + 2*x + 1

# 计算不定积分∫f dx
indefinite_integral = sp.integrate(f, x)
print(indefinite_integral)

# 计算定积分∫_0^1 f dx
definite_integral = sp.integrate(f, (x, 0, 1))
print(definite_integral)

`evalf()`求数值结果

在求积分过程中，我遇到了这样的情况：

1 2	f1 = x/(6+5x*2) print("定积分结果为：",sp.integrate(f1, (x, 0, 12)))

输出的结果是定积分结果为：-log(6)/10 + log(726)/10

这代表的意思是: $-\dfrac{\ln{6}}{10}+\dfrac{\ln{726}}{10}$

可是我想直接输出数值结果，我就可以用evalf()函数

1 2	f1 = x/(6+5x*2) print("用sympy求解的定积分结果为：",sp.integrate(f1, (x, 0, 12)).evalf())

这样写的输出结果就是：

用sympy求解的定积分结果为： 0.479579054559674

SymPy的evalf函数用于将符号表达式的结果转换为具体的数值，这个函数的基本用法如下：
1
>result = some_expression.evalf()
在这里，some_expression是你想要求值的SymPy表达式，evalf函数会返回这个表达式的数值结果。

evalf函数还可以接受一个可选的参数，用于指定结果的精度。例如，some_expression.evalf(50)会返回一个精确到50位有效数字的结果。

此外，evalf函数还可以接受一个名为subs的参数，这是一个字典，用于指定符号变量的值。例如，如果你的表达式中包含符号变量x，你可以这样使用evalf函数：
1
>result = some_expression.evalf(subs={x: 3.14})
在这里，subs={x: 3.14}指定了x的值为3.14。evalf函数会先将x替换为3.14，然后计算表达式的值。

可以看到，evalf函数是用来算数值结果的，一定程度上类似于subs，但与subs的区别在于：

subs和evalf函数在SymPy库中都用于替换和求值，但它们的工作方式有所不同。

subs函数用于替换表达式中的符号变量。例如，f.subs(x, 3)会将表达式f中的所有x替换为3。subs函数返回的是一个新的表达式，这个表达式中的x已经被替换为3。需要注意的是，subs函数不会改变原来的表达式。

evalf函数用于将符号表达式的结果转换为具体的数值。例如，f.evalf()会返回f的数值结果。evalf函数还可以接受一个名为subs的参数，这是一个字典，用于指定符号变量的值。例如，f.evalf(subs={x: 3})会先将f中的x替换为3，然后计算表达式的值。

subs和evalf函数的主要区别在于，subs函数只进行替换，不进行求值，而evalf函数则会进行求值。此外，evalf函数在处理数值精度时比subs函数更加精确。

再比如计算一个很复杂的积分：$\int_0^{1}\sqrt{x}\ln{x}dx$

1
2
3

f2 = sp.sqrt(x) * sp.ln(x)
#注意这个函数在0处的问题，因为lnx在0没定义
print(sp.latex(sp.integrate(f2, (x, 0, 1))))

注：此处用到了sympy的latex函数，可以把一个数值结果转为$\LaTeX$表达式，参数仅仅只需要一个符号表达式即可，此处不过多展开

输出的东西就长这样，我不认识：

$$ \begin{align*} \int\limits_{0}^{1} \begin{cases} 2 \sqrt{x} \log{\left(x \right)} & \text{for}\: \frac{1}{x} < 1 \wedge x < 1 \\\sqrt{x} \log{\left(x \right)} & \text{for}\: \frac{1}{x} < 1 \vee x < 1 \\\frac{{G_{3, 3}^{0, 3}\left(\begin{matrix} \frac{3}{2}, \frac{5}{2}, 1 & \\ & \frac{3}{2}, \frac{3}{2}, 0 \end{matrix} \middle| {x} \right)} + \frac{3 {G_{3, 3}^{0, 3}\left(\begin{matrix} \frac{5}{2}, \frac{5}{2}, 1 & \\ & \frac{3}{2}, \frac{3}{2}, 0 \end{matrix} \middle| {x} \right)}}{2}}{x} - \frac{{G_{3, 3}^{2, 1}\left(\begin{matrix} 0 & \frac{5}{2}, \frac{5}{2} \\\frac{3}{2}, \frac{3}{2} & 0 \end{matrix} \middle| {x} \right)}}{x} & \text{otherwise} \end{cases}\, dx \end{align*} $$

我明明就只想要一个数值结果，你给我这玩意，我咋看啊？

于是就可以用这个evalf函数直接求出数值结果：

f2 = sp.sqrt(x) * sp.ln(x)
#用一个很小的数代替0，因为在0处lnx没有定义
epsilion = 1e-20
print(sp.integrate(f2, (x, epsilion, 1)).evalf())

输出的结果就是我们想要的：-0.444444444444444

数字图像处理

jpg和png

虽然早都知道jpg有损压缩，但是一直只是当成一个小知识点记住的

你妈逼，第二次数字图像处理实验狠狠地给我上了一课，很几把生气

要求很简单，统计灰度值的直方图

def draw_histogram(img):
    # 读取图片
    img = cv2.imread(img, cv2.IMREAD_GRAYSCALE)

    # 计算直方图
    Histogram = np.zeros(256)
    rows, cols = img.shape
    
    for i in range(rows):
        for j in range(cols):
            Histogram[img[i,j]] = Histogram[img[i,j]] + 1

    for i in range(256):
        Histogram[i] = Histogram[i] / img.size

    print(Histogram)
    # 绘制直方图
    plt.bar(np.arange(len(Histogram)), Histogram, width=1.1)
    plt.title("Histogram")
    plt.xlabel('Value')
    plt.ylabel('Frequency')
    plt.show()

原图的直方图长这样：

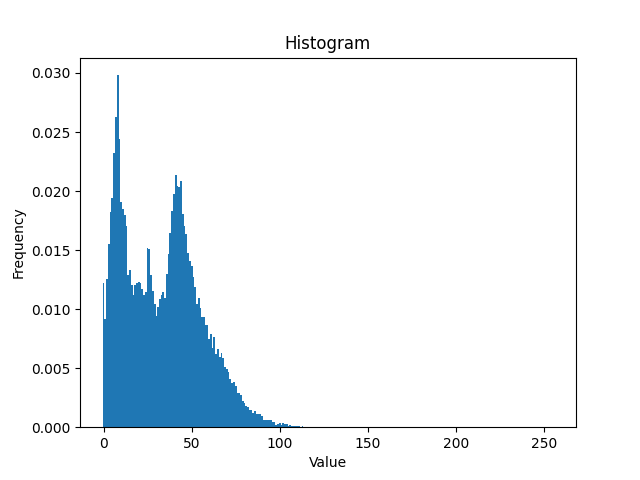
很不错的开始对吧，画的很对是吧？

然而我处理完的图却他妈长这样：

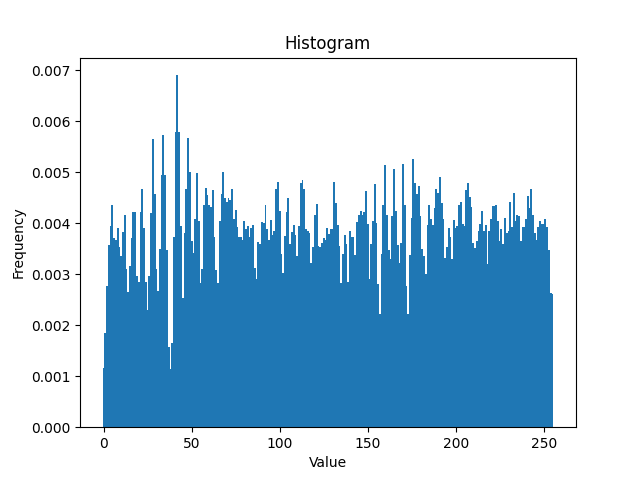
图片，很神奇吧？

我百思不得其解啊，处理完的图像结果跟PPT上的一样，原图的直方图也画的很好，不可能是我函数错了啊？

最后问同学要了他图像处理的结果，一看图片后缀名：.png

就在这一刻，jpg有损压缩这个知识点像他妈闪击波兰的德国一样闪击了我的大脑，脑子里开始有闪电划过，名叫“一个啥b改了两个小时代码”的大纲和分镜如同寒武纪生命大爆发一样缓慢形成，然而愤怒逐渐超过理智占据了上风，于是这个分镜分着分着就变成了他妈的磁场转动100万匹，海虎爆裂拳，狠狠地锤向了桌子。

这是因为PNG和JPG这两种图像格式使用了不同的压缩算法。PNG使用的是无损压缩，这意味着保存为PNG格式的图像不会丢失任何原始图像数据。而JPG使用的是有损压缩，这意味着保存为JPG格式的图像在压缩过程中会丢失一些图像信息。

当你将同一张图像保存为PNG和JPG格式时，由于JPG的有损压缩，可能会导致一些像素值发生改变，这就可能导致两个直方图不完全相同。

此外，JPG的压缩算法在处理高频信息（例如边缘、纹理等）时，可能会引入一些压缩噪声，这也可能影响直方图的结果。

所以，即使你使用的是同一个算法，由于PNG和JPG的压缩方式的差异，得到的直方图可能会有所不同。

所以在我把处理的图像改为.png以后，终于正常了

那么代价是什么呢？也就是我周六晚上的2个小时吧

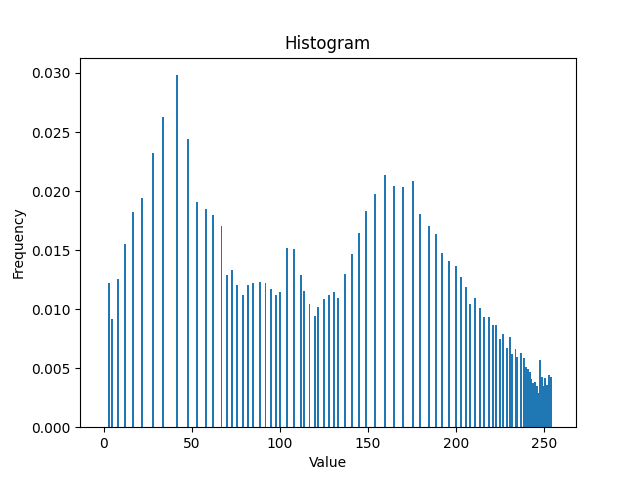
读取彩色图像

我需要读取一张彩色图：

1 2	Mat img4 = imread("实验指导书所用图像和数据\\experiment 3\\experm03_dairyGoatFace.png", CV_8UC3); cout << img4.channels() << endl;

得到的输出是1

在OpenCV中，imread函数的第二个参数是一个标志，用于指定应如何读取图像。CV_8UC3并不是一个有效的标志。如果你想以彩色模式读取图像，你应该使用IMREAD_COLOR标志。如果你想以灰度模式读取图像，你应该使用IMREAD_GRAYSCALE标志。

如果你没有指定标志，或者指定了一个无效的标志，那么imread函数将尝试以彩色模式读取图像。然而，如果图像本身就是一个灰度图像，那么即使你尝试以彩色模式读取它，你得到的仍然会是一个单通道图像。

所以，如果你的图像experm03_dairyGoatFace.png本身就是一个灰度图像，那么无论你如何读取它，你得到的都会是一个单通道图像。你可以通过调用channels函数来检查图像的通道数：
1
2
>Mat img4 = imread("实验指导书所用图像和数据\\experiment 3\\experm03_dairyGoatFace.png", IMREAD_COLOR);
>cout << "Number of channels: " << img4.channels() << endl;
这段代码将输出图像的通道数。如果输出的是1，那么说明你的图像是一个灰度图像。如果输出的是3，那么说明你的图像是一个彩色图像。

前几次实验中也没碰到这种情况，以后知道了：

如果读灰度图，指定参数为IMREAD_GRAYSCALE

如果读彩色图，指定参数为IMREAD_COLOR

而CV_8UC3则可以用来生成一张新的彩色图，同理CV_8UC1可以生成一张新的灰度图

模板卷积范围

看看这个钝化掩膜和高提升滤波的结果，有点难绷对吧

这一步之前做了高斯滤波，给图像做了平滑，没有问题，所以问题出在接下来的一步：高提升滤波

关键问题就在于没有保证最后每个通道都在0-255

因为模板卷积的结果很可能超出[0,255]这个区间，所以在最后赋值的时候需要做一步判断：超过255的赋值为255，低于0的赋值0

就是这样的操作：min(max((int)(src.at<Vec3b>(i, j)[0] + k * Masking_B[i][j]), 0), 255)

其中min()和max()函数用到了cmath库

这块处理的代码如下

//生成掩膜
vector<vector<int>> Masking_B(src.rows, vector<int>(src.cols, 0));
vector<vector<int>> Masking_G(src.rows, vector<int>(src.cols, 0));
vector<vector<int>> Masking_R(src.rows, vector<int>(src.cols, 0));
for (int i = 0; i < src.rows; i++)
{
    for (int j = 0; j < src.cols; j++)
    {
        Masking_B[i][j] = src.at<Vec3b>(i, j)[0] - Gaussian_filterimg.at<Vec3b>(i, j)[0];
        Masking_G[i][j] = src.at<Vec3b>(i, j)[1] - Gaussian_filterimg.at<Vec3b>(i, j)[1];
        Masking_R[i][j] = src.at<Vec3b>(i, j)[2] - Gaussian_filterimg.at<Vec3b>(i, j)[2];
    }
}

//得到钝化滤波结果
for (int i = 0; i < src.rows; i++)
{
    for (int j = 0; j < src.cols; j++)
    {
        //保证最后每个通道都在0-255
        dest.at<Vec3b>(i, j)[0] = min(max((int)(src.at<Vec3b>(i, j)[0] + k * Masking_B[i][j]), 0), 255);
        dest.at<Vec3b>(i, j)[1] = min(max((int)(src.at<Vec3b>(i, j)[1] + k * Masking_G[i][j]), 0), 255);
        dest.at<Vec3b>(i, j)[2] = min(max((int)(src.at<Vec3b>(i, j)[2] + k * Masking_R[i][j]), 0), 255);
    }
}

C++中指针释放问题

我现在有一个函数：

//对一个一维MyComplex数组傅里叶变换
//返回的参数为result
MyComplex* MyFourier(int N, MyComplex* Array)
{
	MyComplex List[defaultSize][defaultSize];
	MyComplex* result = new MyComplex[N];

	double PI = acos(-1);

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			List[i][j] = MyComplex(cos(-2 * PI / N * i * j), sin(-2 * PI / N * i * j));
		}
	}

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			result[i] = result[i].Add(List[i][j].Mult(Array[j]));
			if (abs(result[i].real) < 1e-10)		result[i].real = 0;
			if (abs(result[i].imagin) < 1e-10)		result[i].imagin = 0;
		}
	}
	return result;
}

这个函数内部实现了MyComplex* result = new MyComplex[N];

最后把这个指针return了，给另外的函数计算用

现在我需要在一个新函数中调用这段函数，我应该在初始化这个指针时赋值为空：

void MyFourier_image(int** image, int width, int height, int axis = 0)
{
	float PixelArray_float[defaultSize] = { 0 };
	MyComplex PixelArray_MyComplex[defaultSize];

	MyComplex* resultTemp = NULL;		//这里要记得初始化为NULL或者nullptr
    ...
        resultTemp = MyFourier(width, PixelArray_MyComplex);
    ...
    //释放
    if(resultTemp != nullptr) 
    {
        delete[] resultTemp;
        resultTemp = nullptr;
	}
    ...
}

释放后记得置为空

关于NULL和nullptr的问题：

在C++中，NULL和nullptr都可以用来表示空指针，但它们并不完全相同。

NULL是C语言中的一个宏，通常被定义为整数0。在C++中，NULL也可以用来表示空指针，但因为它实际上是一个整数，所以在某些情况下可能会引发问题。例如，如果你有一个函数重载，一个接受int参数，一个接受指针参数，那么使用NULL作为参数可能会调用错误的函数。

nullptr是C++11引入的一个新关键字，用来表示空指针。它的类型是std::nullptr_t，可以隐式转换为所有指针类型，但不能转换为其他类型，如int。因此，使用nullptr可以避免上述NULL可能引发的问题。

总的来说，如果你正在编写C++代码，推荐使用nullptr来表示空指针。如果你正在维护旧的C++代码，或者需要与C语言代码兼容，那么可能会看到NULL。但是，你应该尽量避免在新的C++代码中使用NULL。如果你需要表示空指针，应该使用nullptr。这是一种更安全，更具表现力的方式。

频域

先说直观感受：我真是草了，频域真几把麻烦

DFT与IDFT

我还是没搞明白，挺麻烦的，这里只记录能够实现功能的代码

DFT:

//DFT，把中间的img_DFT也传出去
//传入一张正常的图img
//第二个形参是传出一个img_DFT，作IDFT用
//return能正常显示（对数尺度，归一化），正常imwrite（转换到0到255的范围并转换为8位无符号整型）
Mat MyDFT(Mat& img, Mat& img_DFT)
{
	Mat img_float;
	img.convertTo(img_float, CV_32F);  // 转换为浮点类型

	// 进行傅里叶变换
	dft(img_float, img_DFT);

	//计算幅度
	Mat planes[] = { Mat::zeros(img_DFT.size(), CV_32F), Mat::zeros(img_DFT.size(), CV_32F) };
	split(img_DFT, planes);  // 分离实部和虚部
	magnitude(planes[0], planes[1], planes[0]);  // 计算幅度
	Mat Magnitude = planes[0];

	//转换为对数尺度
	Magnitude += Scalar::all(1);
	log(Magnitude, Magnitude);
    
    //上面计算了傅立叶变换的幅度，并将其转换为对数尺度
	//因为傅立叶变换的结果是复数，而我们通常关心的是每个频率分量的幅度

	//归一化，以便于显示
	normalize(Magnitude, Magnitude, 0, 1, NORM_MINMAX);

	//转换到0到255的范围并转换为8位无符号整型
	//如果不加这个，imwrite就会是全黑的
	Magnitude.convertTo(Magnitude, CV_8U, 255.0);
	
    //归一化和转换到0到255的范围，这是为了能够将结果显示为图像
    
	return Magnitude;
}

如果不加Magnitude.convertTo(Magnitude, CV_8U, 255.0);，最后在程序中的imshow能正常显示，但是imwrite以后却是全黑的

计算了傅立叶变换的幅度，并将其转换为对数尺度。

这是因为傅立叶变换的结果是复数，而我们通常关心的是每个频率分量的幅度。

然后，你进行了归一化和转换到0到255的范围，这是为了能够将结果显示为图像。

IDFT:

//IDFT，传入的应该是img_DFT
//img_DFT 应该没做任何处理，直接是 dft(img_float, img_DFT) 输出的参数
//img_DFT 保存了傅立叶变换的结果，这是一个复数矩阵
//计算幅度和进行对数转换后，返回的Mat只包含了这个复数矩阵的幅度信息，丢失了相位信息，不能正常IDFT
Mat MyIDFT(Mat& img_DFT)
{
	// 进行傅里叶反变换
	Mat img_idft;
	idft(img_DFT, img_idft, DFT_SCALE | DFT_REAL_OUTPUT);
	img_idft.convertTo(img_idft, CV_8U); // 转换为8位无符号整型

	return img_idft;
}

不能直接把刚刚return的图片直接进来IDFT：

在你的代码中，你首先对图像进行了傅立叶变换（DFT），然后计算了幅度，并将其转换为对数尺度。这个过程改变了原始DFT结果的复数结构，因此你不能直接对这个结果进行逆傅立叶变换（IDFT）。

当你调用 dft(img_float, img_DFT); 时，img_DFT 保存了傅立叶变换的结果，这是一个复数矩阵。而当你计算幅度和进行对数转换后，Magnitude 只包含了这个复数矩阵的幅度信息，丢失了相位信息。因此，你不能直接对 Magnitude 进行IDFT。

频域滤波

紧接着刚刚的DFT与IDFT，现在又加了几个新要求：

首先对其进行频率域平移的傅里叶变换，接着再分别进行低通滤波、高通滤波和巴特沃斯滤波，最后分别对滤波的结果再进行逆傅里叶变换，得到滤波结果

频域平移还是很好实现的：

//四角移动，频域移动
void shiftDFT(Mat& img_DFT)
{
	int cx = img_DFT.cols / 2;
	int cy = img_DFT.rows / 2;

	Mat q0(img_DFT, Rect(0, 0, cx, cy));
	Mat q1(img_DFT, Rect(cx, 0, cx, cy));
	Mat q2(img_DFT, Rect(0, cy, cx, cy));
	Mat q3(img_DFT, Rect(cx, cy, cx, cy));

	Mat tmp;
	q0.copyTo(tmp);
	q3.copyTo(q0);
	tmp.copyTo(q3);

	q1.copyTo(tmp);
	q2.copyTo(q1);
	tmp.copyTo(q2);
}

关于滤波，我一开始是这样写的：

//这是错误的写法，得到的是错误的结果

Mat img2 = imread("实验指导书所用图像和数据\\experiment 5\\experm05_flower.png", IMREAD_GRAYSCALE);
Mat img2_shift_DFT = img2.clone();
Mat img2_DFT_readable = MyDFT(img2, img2_shift_DFT);

//频移DFT
shiftDFT(img2_shift_DFT);

//频移后IDFT
Mat img2_shift_IDFT = MyIDFT(img2_shift_DFT);
imshow("img2ShiftIDFT", img2_shift_IDFT);

//低通滤波
Mat img2_shift_DFT_blur = img2_shift_DFT.clone();
blur(img2_shift_DFT, img2_shift_DFT_blur, Size(3, 3));
imshow("img2_shift_blur", img2_shift_DFT_blur);

//逆变换
Mat img2_shift_blur_IDFT = MyIDFT(img2_shift_DFT_blur);
imshow("img2_shift_IDFT_blur_IDFT", img2_shift_blur_IDFT);
imwrite("Result\\experiment 5\\img2_shift_blur_IDFT.png", img2_shift_blur_IDFT);

得到了一张很奇怪的图：

太几把怪了，我就去问了bing，解答如下：

你的代码中，低通滤波的部分可能存在一些问题。你在傅立叶变换的结果上应用了blur()函数，这可能会导致结果不正确。因为blur()函数是在空间域进行操作的，而不是在频率域。

在频率域进行滤波，通常的做法是创建一个滤波器，然后将其与傅立叶变换的结果相乘。例如，你可以创建一个低通滤波器，它在中心附近的值为1，在远离中心的地方逐渐变为0。然后，你可以将这个滤波器与img2_shift_DFT相乘，从而实现低通滤波。

问题就在于我的滤波是对空间域滤波，而不是对频率域滤波

正确的写法如下：

Mat img2 = imread("实验指导书所用图像和数据\\experiment 5\\experm05_flower.png", IMREAD_GRAYSCALE);
Mat img2_shift_DFT = img2.clone();
Mat img2_DFT_readable = MyDFT(img2, img2_shift_DFT);

//频移DFT
shiftDFT(img2_shift_DFT);

//频移后IDFT
Mat img2_shift_IDFT = MyIDFT(img2_shift_DFT);
imshow("img2ShiftIDFT", img2_shift_IDFT);

// 创建滤波器
Mat Low_pass_filter = Mat(img2_shift_DFT.rows, img2_shift_DFT.cols, CV_32F);
float D0 = 50.0;  // 截止频率
for (int i = 0; i < img2_shift_DFT.rows; i++)
{
	for (int j = 0; j < img2_shift_DFT.cols; j++)
	{
		float D = sqrt(pow(i - img2_shift_DFT.rows / 2.0, 2) + pow(j - img2_shift_DFT.cols / 2.0, 2));
		Low_pass_filter.at<float>(i, j) = exp(-(D * D) / (2 * D0 * D0));
	}
}

// 应用滤波器
Mat img2_DFT_filtered;
multiply(img2_shift_DFT, Low_pass_filter, img2_DFT_filtered);

// 逆傅立叶变换
Mat img2_shift_Lowpassfiltered = MyIDFT(img2_DFT_filtered);
imshow("img2_shift_Lowpassfiltered", img2_shift_Lowpassfiltered);
imwrite("Result\\experiment 5\\img2_shift_Lowpassfiltered.png", img2_shift_Lowpassfiltered);

得到了一看就很正常的结果：

DCT

离散余弦变换

很几把搞笑

//笑死我了这个函数
//是否归一化会影响到imshow和imwrite
//我的解决方法就是直接指定哪个图用来imwrite，哪个图用来imshow
void MyDCT(Mat& img, Mat& img_DCT_imwrite, Mat& img_DCT_imshow)
{
	//img.convertTo(img, CV_32F, 1.0 / 255);		//这样写imshow正确imwrite全黑
	//img.convertTo(img, CV_32F);					//这样写imwrite正确imshow花屏

	Mat imgTemp = img.clone();

	img.convertTo(img, CV_32F);						//imwrite正确
	imgTemp.convertTo(imgTemp, CV_32F, 1.0 / 255);		//imshow正确

	dct(img, img_DCT_imwrite);
	dct(imgTemp, img_DCT_imshow);
}

我他妈用img.convertTo(img, CV_32F, 1.0 / 255);的时候，imshow正确imwrite全黑

我用img.convertTo(img, CV_32F);的时候imwrite正确imshow花屏

给哥们整不会了

我直接左右开弓，他妈的你不是又要imshow又要imwrite吗？我就给你对应正确的

有了DCT，紧接着就是IDCT

经过测试，只有idct(img_DCT_imshow, img_IDCT)才能正常显示，idct(img_DCT_imwrite, img_IDCT)得到的是全白图片

参考资料

Pandas 教程 | 菜鸟教程 (runoob.com)

如何用一行代码打败修炼三十年的高数老师 [南京大学 IT 侠 iTalk]

Python问题

pandas库记录

Series

索引对齐问题

元素级别的乘法

DataFrame

矩阵乘法

numpy库记录

生成序列

axis

找最小值和对应的下标

np.zeros()生成指定数组

矩阵相关

逆矩阵

转置矩阵

矩阵乘法

获取矩阵行列信息

reshape()函数

numpy特有的下标访问方法

特殊下标

:切片功能

引用赋值

matplotlib.pyplot库记录

重置一张图片

用来正常显示负号和中文

指定坐标轴

保存图片

sympy库记录

subs()函数替换

integrate()积分

evalf()求数值结果

数字图像处理

jpg和png

读取彩色图像

模板卷积范围

C++中指针释放问题

频域

DFT与IDFT

频域滤波

DCT

参考资料

`axis`

`np.zeros()`生成指定数组

`reshape()`函数

`:`切片功能

`subs()`函数替换

`integrate()`积分

`evalf()`求数值结果