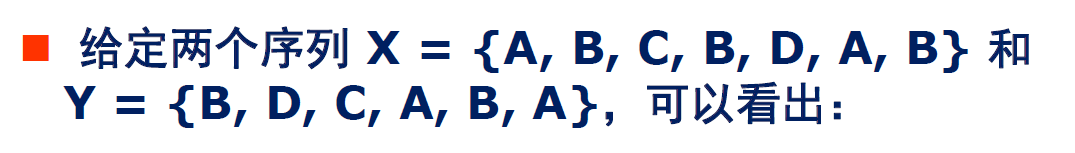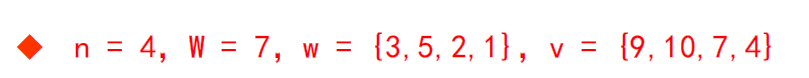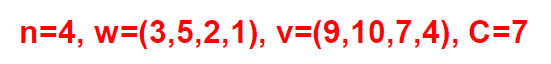算法分析与设计复习整理
算法引论
算法
算法的定义
(串讲强调)
算法:对于计算机科学来说,算法指的是针对特定问题求解步骤的一种描述,是包含若干条指令的一个有穷序列
算法的特性
输入(0或多个)
输出(至少1个)
确定性(无歧义)
有限性
可行性
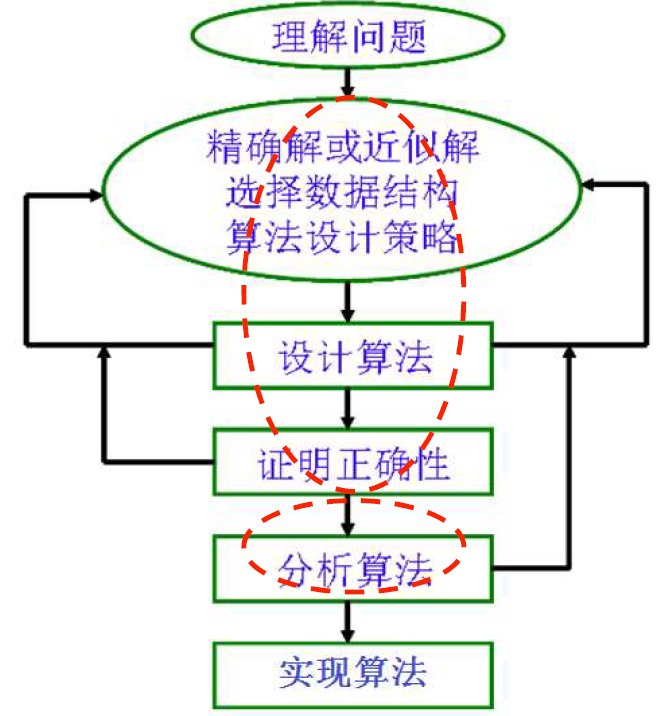
算法设计一般过程
算法描述方法——伪代码
算法复杂性分析
时间复杂度
时间复杂性(影响因素包括问题规模n、输入序列I、算法本身A)
算法的渐近复杂性:
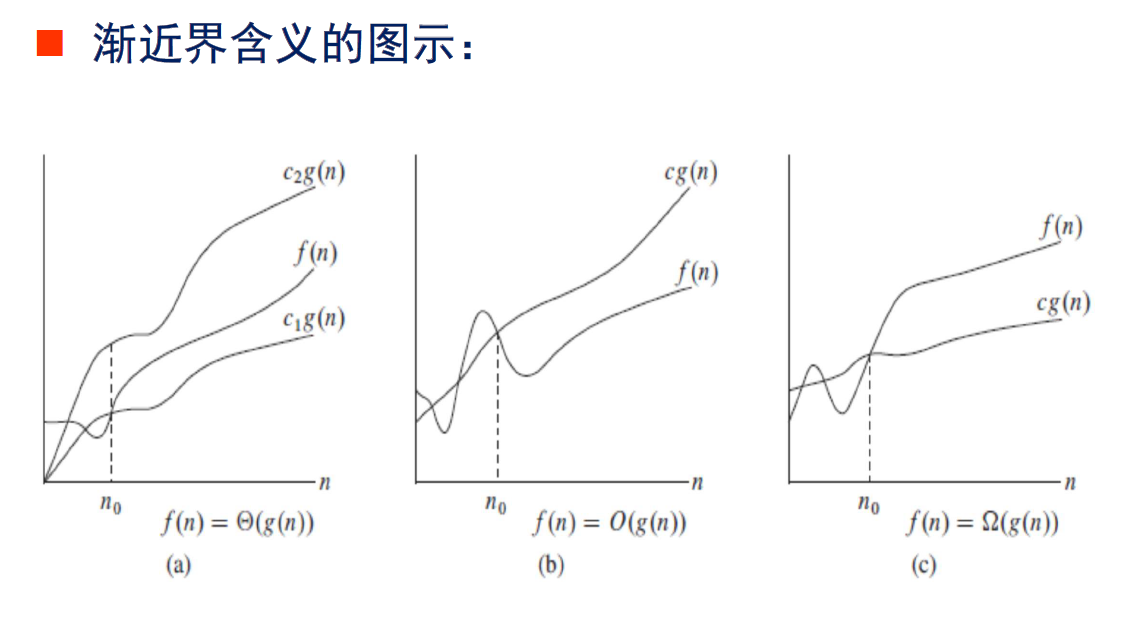
渐近意义下的记号
渐近上界:\(f(n)=O(g(n))\)
即\(f(n)\) 的阶不高于 \(g(n)\) 的阶
渐近下界:\(f(n)=\Omega(g(n))\)
即\(f(n)\) 的阶不低于 \(g(n)\) 的阶
渐近紧确界:存在正的常数\(c_1,c_2\) ,使\(n\) 大时,满足\(c_1g(n)\le f(n)\le c_2g(n)\)
即\(f(n)\) 与\(g(n)\) 同阶
几类复杂性之间的关系
非递归,递归
空间复杂度
空间复杂度(影响因素包括输入输出数据IO、辅助变量V、算法本身A)
算辅助变量
递归与分治策略
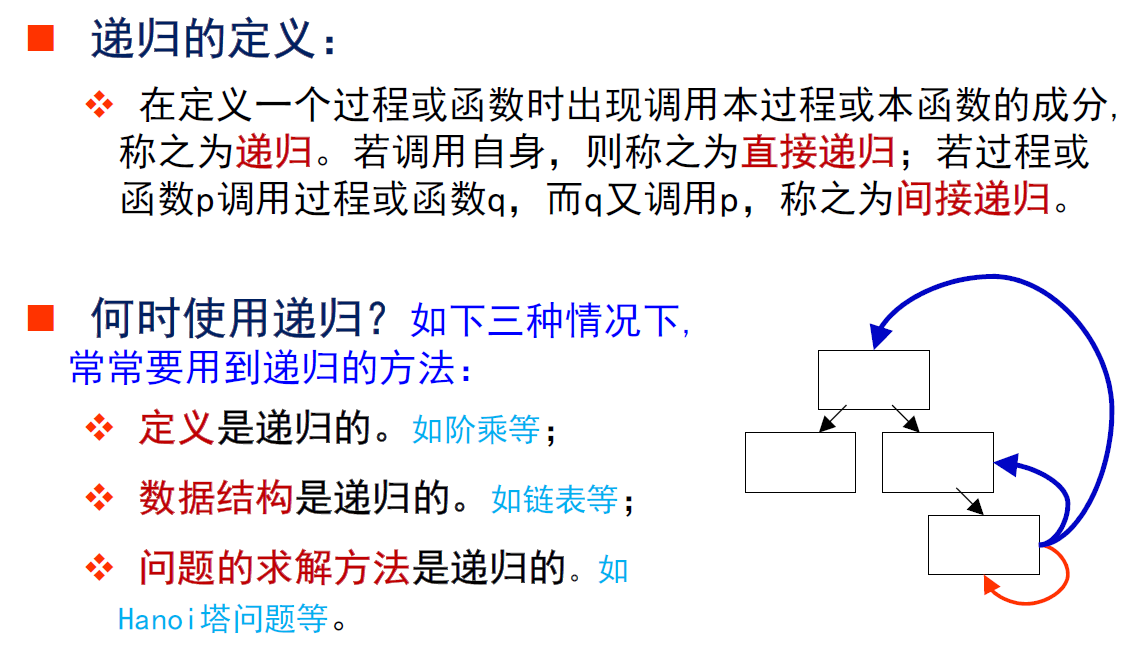
递归
递归时间复杂度
主定理
主定理适用范围:分治 ,如果是递归非分治(如阶乘,斐波那契数列)就不能用主定理(求阶乘拿主定理算的是\(O(\log n)\) ,但是阶乘的复杂度为\(O(n)\) ) \[
\begin{align*}
T(n)&=aT(\frac{n}{b})+cn^k\\\\
T(1)&=c\\\\
a,b,c,k都是常量,&则
\begin{cases}
T(n)\in\Theta(n^k)\qquad &\text{if } (a<b^k)\\\\
T(n)\in\Theta(n^k\log n)\qquad &\text{if } (a=b^k)\\\\
T(n)\in\Theta(n^{\log_ba})\qquad &\text{if } (a>b^k)\\
\end{cases}
\end{align*}
\]
参考:
主定理
用主定理解阶乘递归算法的复杂度
递归树
后向带入法
代入法
分治
分治法基本步骤
用分治必须保证最优子结构性质
最优子结构性质
最优子结构性质:一个问题的最优解包含其子问题的最优解
归并排序
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 MergeSort(Arr, Start, End) 输入:Arr数组,起始下标Start,终止下标End 输出:按递增顺序排好的数组 1. if End <= Start //当待排序数组只有一个元素时,就是有序,直接退出 2. return 3. Mid <- (Start + End) / 2 4. MergeSort(Arr, Start, Mid) 5. MergeSort(Arr, Mid + 1, End) 6. Merge(Arr, Start, Mid, End) Merge(Arr, Start, Mid, End) 输入:Arr数组,起始下标Start,中间数Mid,终止下标End 输出:合并好的数组 1. L = Arr[Start...Mid] 2. R = Arr[Mid + 1...End] 3. L.append(无穷) //哨兵,可以保证一个数组遍历完后另一个能继续遍历 4. R.append(无穷) 5. i <- 0, j <- 0, k <- Start 6. while k != End + 1 7. if L[i] <= R[j] 8. Arr[k] <- L[i] 9. i <- i + 1 10. else 11. Arr[k] <- R[j] 12. j <- j + 1 13. k <- k + 1
时间复杂度
空间复杂度
参考:归并排序
快速排序
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 QuickSort(Arr, Start, End) 输入:Arr数组,开始下标Start,结束下标End 输出:升序排序的Arr数组 1. if End <= Start 2. return 3. Index = Partition(Arr, Start, End) 4. QuickSort(Arr, Start, Index - 1) 5. QuickSort(Arr, Index + 1, End) Partition(Arr, Start, End) //经过Partition,有一个元素已经找到位置 输入:Arr数组,开始下标Start,结束下标End 输出:基准元素对应的下标: j (以Arr[End]为基准元素,即没有随机选) 1. for i <- Start to End - 1 2. if Arr[i] <= Arr[End] //从左向右遍历,若小于等于基准元素就交换 3. Swap(Arr[j], Arr[i]) //保证j左边元素全是小于等于基准元素的 4. j <- j + 1 //j到i是大于基准元素的 5. Swap(Arr[End], Arr[j]) //此时j的位置就是基准元素对应位置的下标,交换 6. return j
时间复杂度
最坏情况下,时间复杂度为\(O(n^2)\)
平均情况和最好情况,时间复杂度为\(O(n\log
n)\)
空间复杂度
最坏情况下,递归栈深度为n,空间复杂度为\(O(n)\)
平均情况和最好情况,递归栈深度为\(\log
n\) ,空间复杂度为\(O(\log
n)\)
参考:快速排序
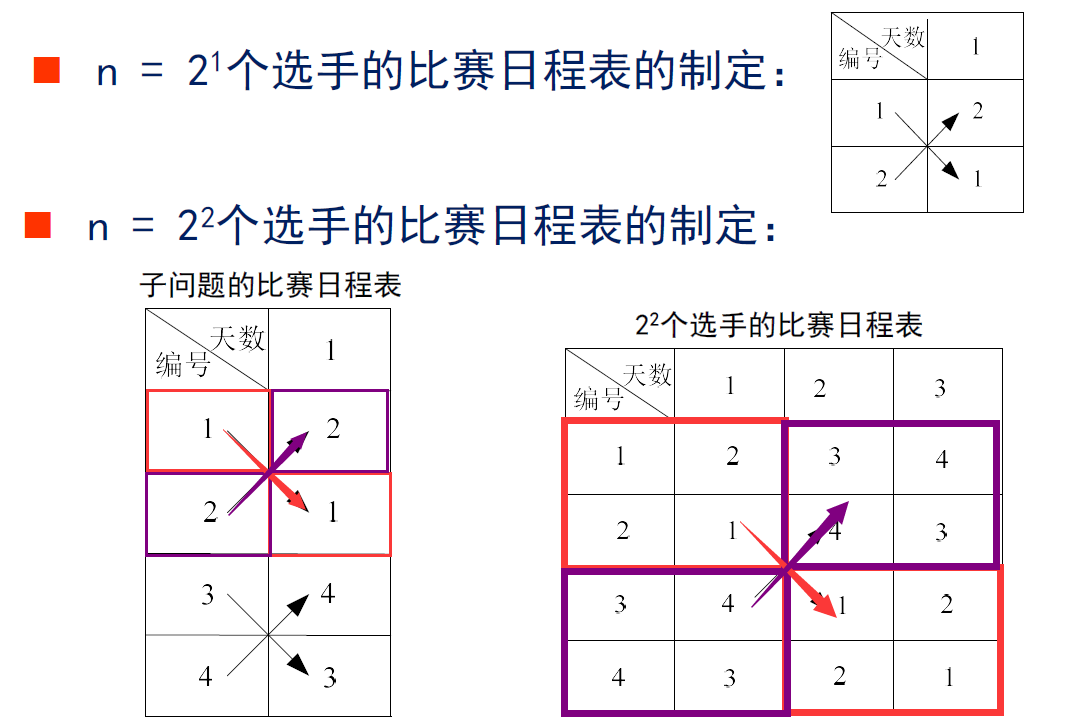
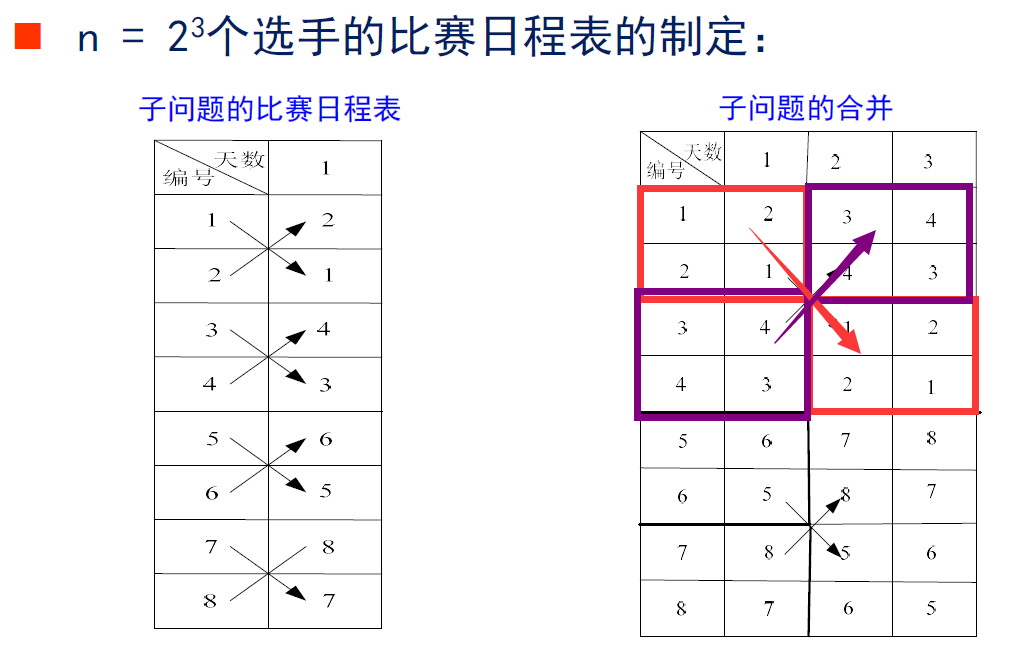
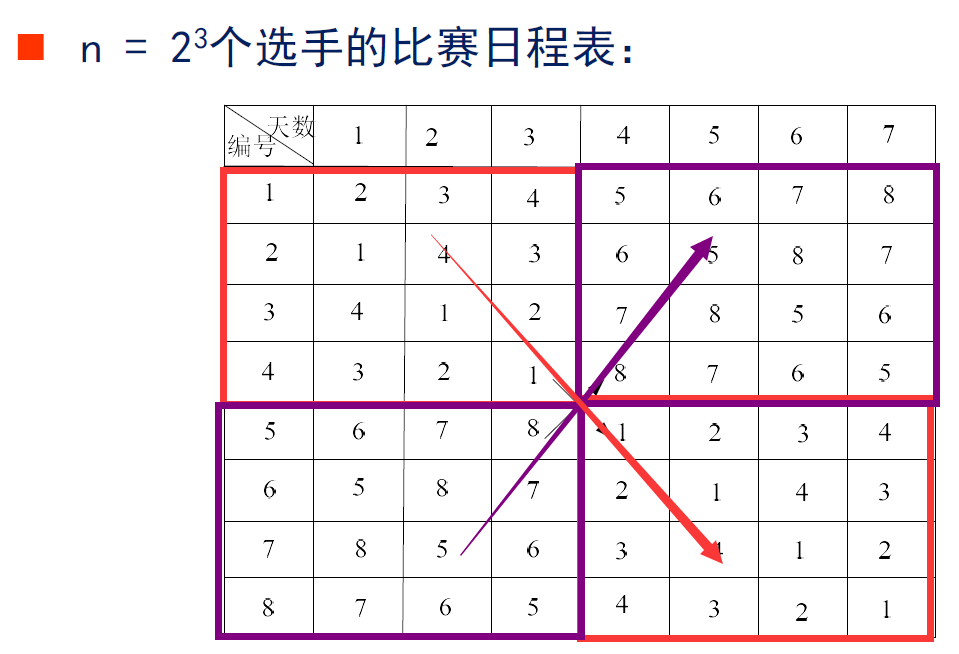
循环日程表
思路:分治,分到2个人就好划分
伪代码
时间复杂度
主定理:\(a=1,b=2,k=2,a<b^k,T(n)=O(n^2)\)
空间复杂度
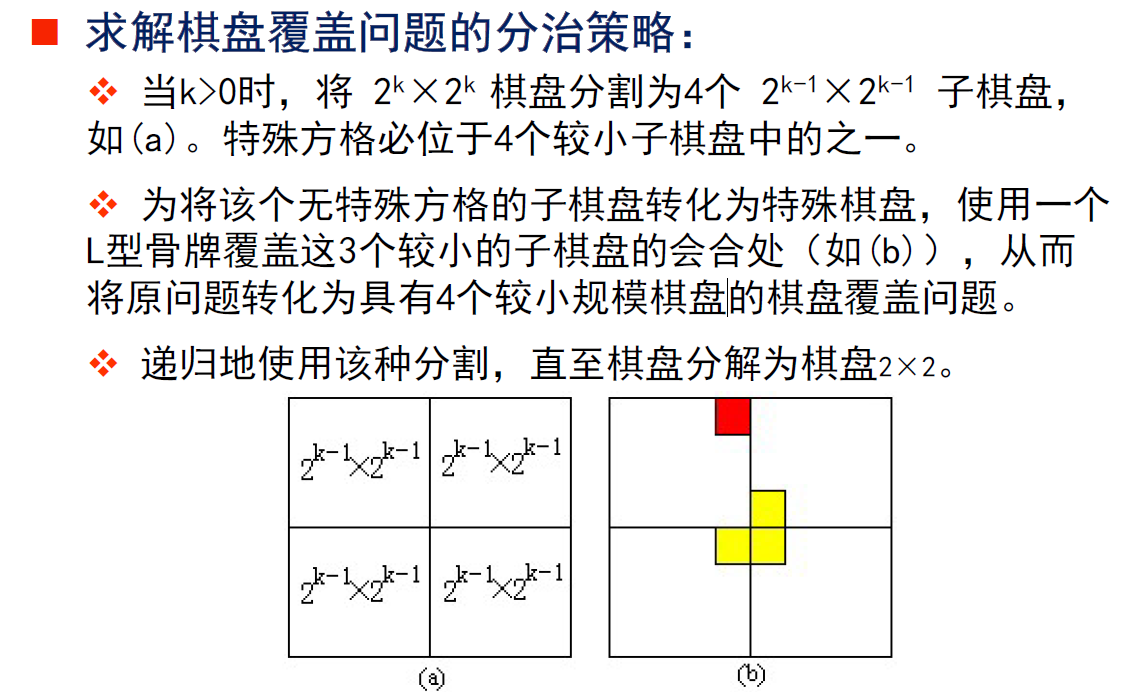
棋盘覆盖问题
注意预处理
时空复杂度
动态规划
满足条件
最优子结构性质
子问题重叠(子问题重复求解)
自底向上
动态规划与分治法异同
相同点:都是基于分治思想
不同点:分治法各个子问题独立,动态规划中允许子问题重叠
求解步骤
根据最优子结构性质,得到动态规划方程
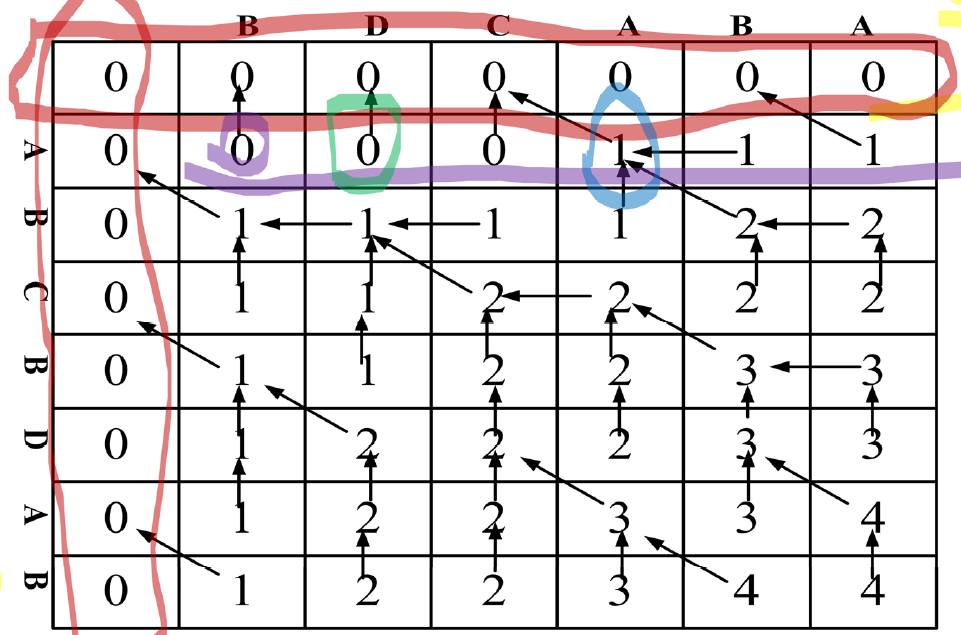
最长公共子序列问题
问题分析
建立方程
注意\(C[i][j]\) 的概念:记录的是\(X_i\) 和\(Y_j\) 最长公共子序列的长度
所以长度为0时,LCS=0
如果碰到相等的,就加1
如果不等,就取\(X_{i-1}\) 和\(Y_j\) 的LCS与\(X_i\) 和\(Y_{j-1}\) 的LCS之间最大值
\(b[i][j]\) 记录子问题最优解的来源,1,2,3为自己规定的方向
图示
伪代码
时间复杂度:两层循环,\(O(n^2)\)
构造解:顺着箭头方向走,遇到斜上方的就是子串序列里的一位
时间复杂性
求解LCS:\(O(n^2)\)
构造解:\(O(n)\)
主程序:\(O(n^2)\)
空间复杂性
求解LCS:\(O(1)\)
构造解:\(O(n)\)
主程序:\(O(n^2)\)
矩阵连乘
问题分析
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 Matrix_Chain_DP(Num, P, DP, S) 输入:矩阵个数Num,矩阵维度数组P(P[i-1]为第i个矩阵的行,P[i]为第i个矩阵的列),动态规划表DP(初始值全为正无穷),最优决策表S(用于记录括号位置) 输出:DP数组(DP[i][j]记录了第i个矩阵乘到第j个矩阵乘法次数最小值)和S数组(S[i][j]记录了第i个矩阵乘到第j个矩阵乘法次数最小值时加括号的位置) 1. for i <- 1 to Num //先初始化DP[i][i],单独一个矩阵乘法次数为0次 2. DP[i][i] <- 0 3. for L <- 2 to Num //L为子串长度,从2到Num 4. for i <- 1 to Num 5. j <- i + L - 1 //j靠i与L决定,从填表顺序推出来的,即DP[1][2]到DP[Num-1][Num]后再从DP[1][3]开始 6. if j > Num 7. break 8. for k <- i to j - 1 //遍历能加括号的所有位置 9. Min <- DP[i][j] //可优化掉Min,放Min只是为了比较大小 10. Temp <- DP[i][k] + DP[k + 1][j] + P[i - 1] * P[k] * P[j] 11. if Temp < Min 12. Min <- Temp 13. DP[i][j] <- Temp 14. S[i][j] <- k 15. return DP and S Print_Chain(S, i, j) 1. if i == j 2. print "A[" + i + "]" 3. else 4. print "(" 5. Print_Chain(S, i, s[i][j]) 6. Print_Chain(S, s[i][j] + 1, j) 7. print ")"
时间复杂度
DP: \(O(n^3)\)
Print: \(O(n)\)
主程序:\(O(n^3)\)
空间复杂度
DP: \(O(1)\)
Print: \(O(n)\)
主程序:\(O(n^2)\)
空间复杂度不考虑输入和输出,但是主程序里创建的DP二维数组和S二维数组仍然是占了空间,所以主程序中空间复杂度为\(O(n^2)\)
参考:矩阵连乘
0-1背包
\(C[i][j]\) 存的是第 \(i\) 件物品,当前背包容量为 \(j\) 时的最佳价值
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Knapsack_01_DP() //自底向上查找最佳价值 输入: Weight数组,Value数组,C数组(初始值全为0) 输出: C数组 (C[i][j]存的是前i件物品,当前背包容量为j时的最佳价值) 1. for i <- 1 to N 2. for j <- 1 to W 3. if j >= Weight[i] 4. C[i][j] <- FindMax(C[i - 1][j], C[i - 1][j - Weight[i]] + Value[i]) 5. else 6. C[i][j] <- C[i - 1][j] GetSolution() //根据二维数组C求解放入背包的物品 输入: C数组 输出: Solution数组 1. j <- W 2. for i <- N to 0 3. if C[i][j] != C[i - 1][j] 4. Solution[i] <- 1 5. j <- j - Weight[i]
时间复杂度
DP: \(O(nW)\)
GetSolution: \(O(n)\)
主程序:\(O(nW)\)
空间复杂度
DP: \(O(1)\)
GetSolution: \(O(1)\)
主程序:\(O(n^2)\)
主程序里开了C二维数组
贪心算法
满足条件
最优子结构性质
贪心选择性质
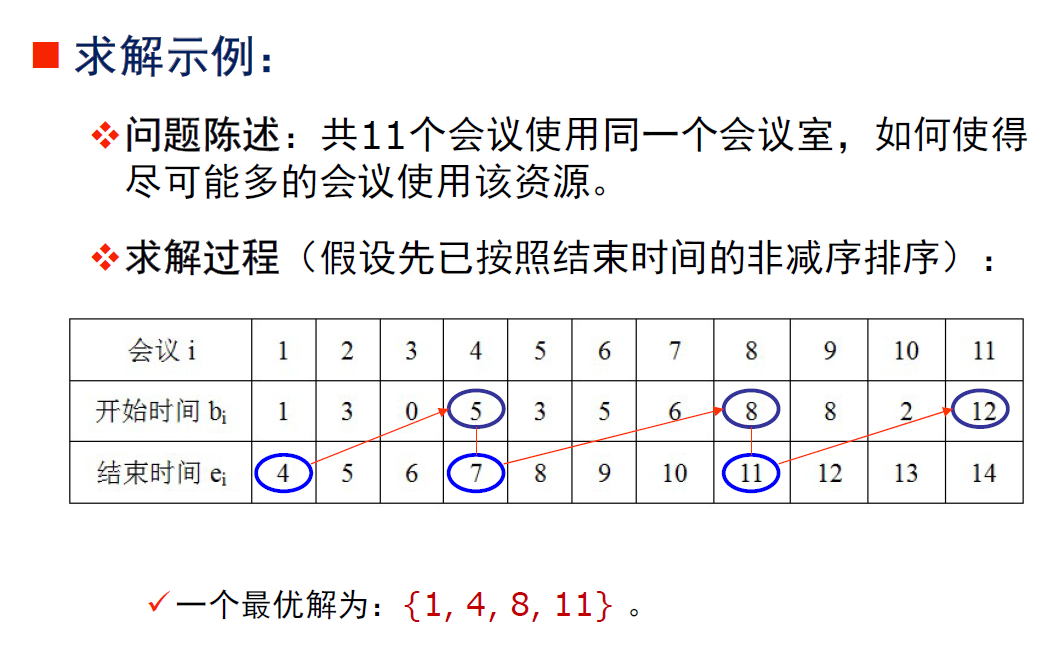
会场安排问题
伪代码
时空复杂度
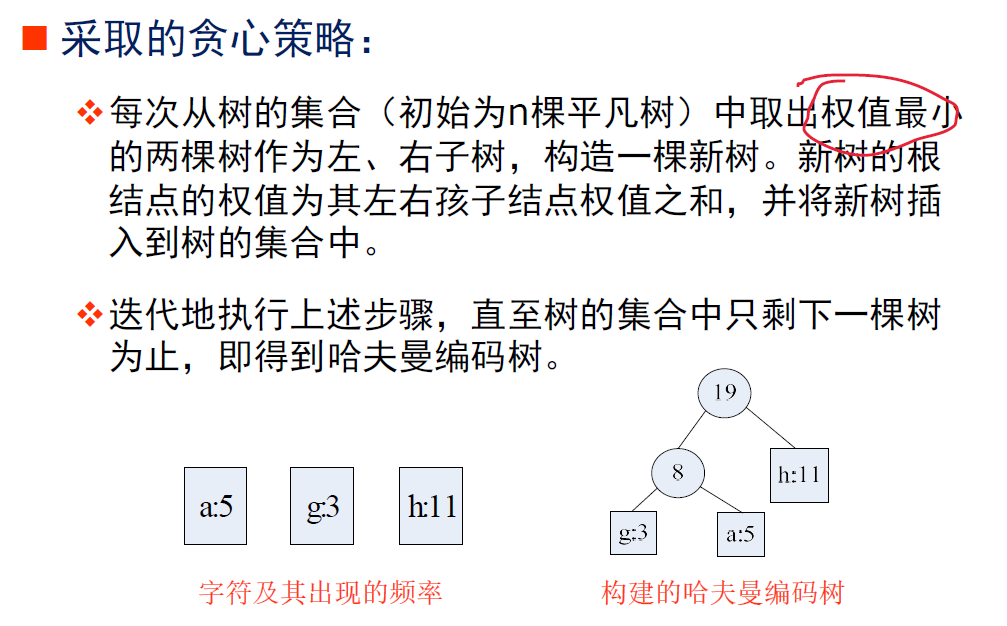
哈夫曼编码
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 BuildTree() 输入: LetterNode类型的List数组 输出: 加入了新节点的List数组 1. LetterNode* LNode 2. LetterNode* RNode 3. while head != tail - 1 4. MySort() 5. DeQueue(LNode) 6. DeQueue(RNode) 7. LetterNode* NewNode <- new LetterNode('0', LNode->num + RNode->num) 8. NewNode->lchild <- LNode 9. NewNode->rchild <- RNode 10. EnQueue(NewNode) AddString_Pre(LetterNode* subroot, string str) //类似前序遍历 输入: subroot, 哈夫曼编码str 输出: Result数组 1. if subroot == NULL 2. return 3. subroot->Huffman <- str 4. if subroot->letter != '0' 5. Result[Result_index] <- *subroot 6. Result_index++ 7. AddString_Pre(subroot->lchild, str + "0") 8. AddString_Pre(subroot->rchild, str + "1") AddString() 输入: List数组 输出: Result数组 1. this->AddString_Pre(&this->List[head], "")
时空复杂度
单源最短路径
特殊路径
(串讲强调)
特殊路径:从源点出发只经过S中的结点到达V-S中的结点的路径
最小生成树
Prim算法
伪代码
时空复杂度
Kruskal算法
伪代码
时空复杂度
参考:最小生成树
回溯法
三种解空间树
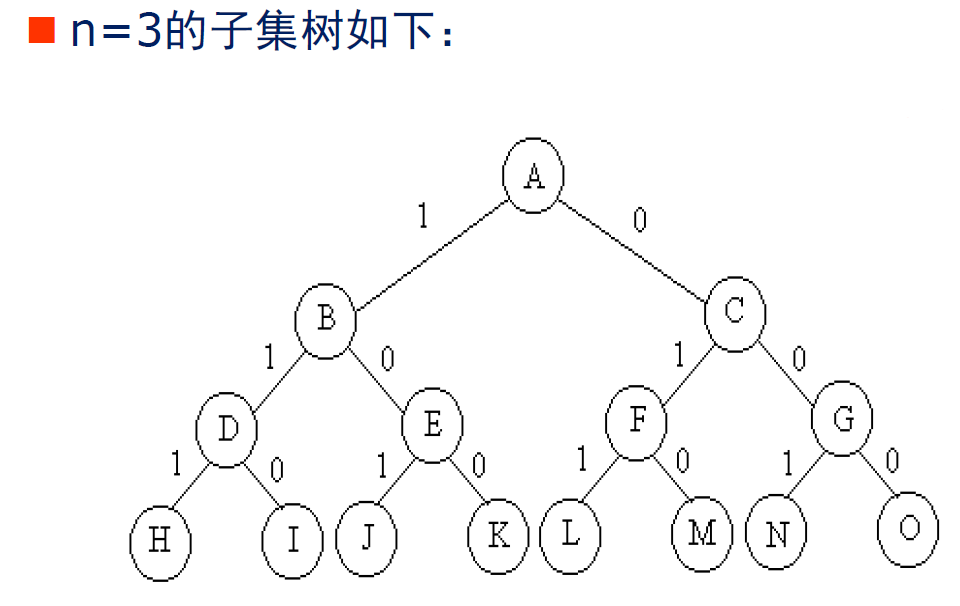
子集树
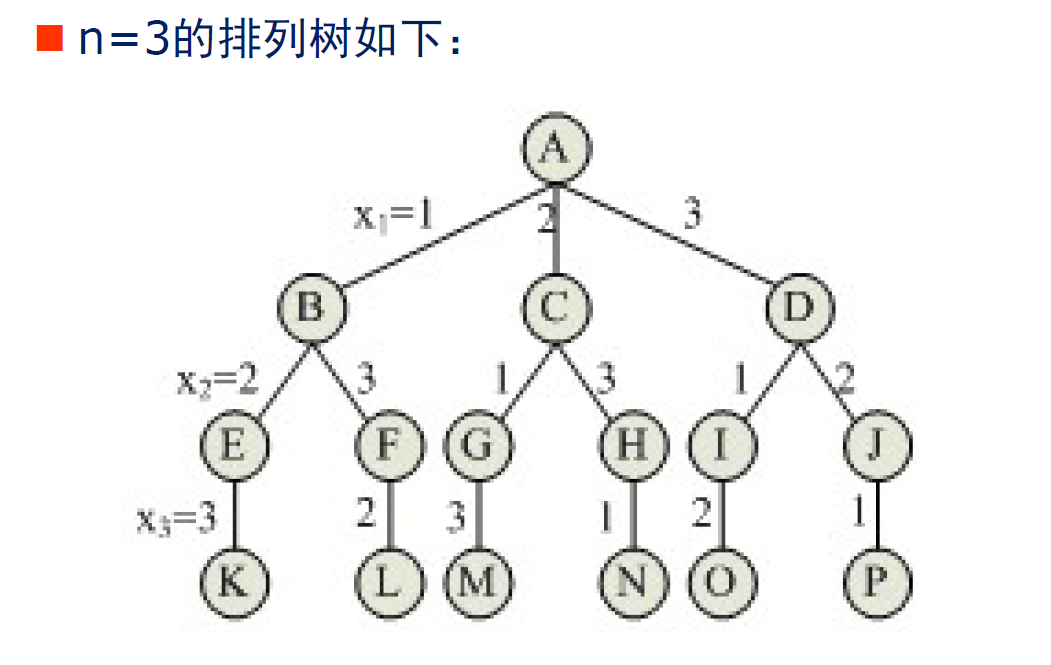
排列树
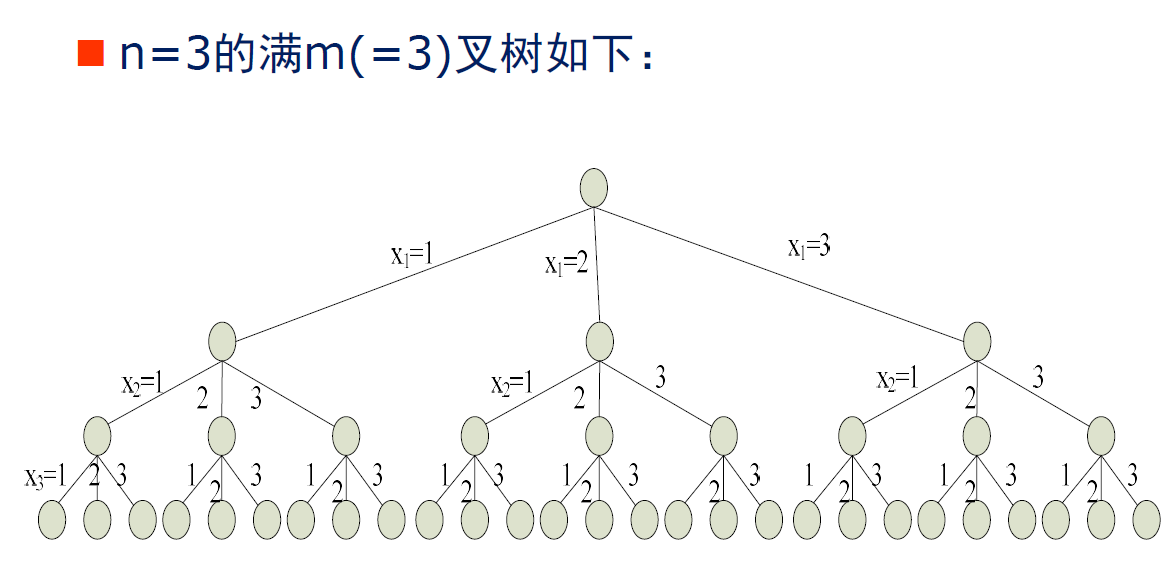
满m叉树
子集树
排列树
满m叉树
解空间树剪枝函数
解空间树三种节点
回溯法求解步骤
子集树递归回溯伪代码
排列树递归回溯伪代码
满m叉树递归回溯伪代码
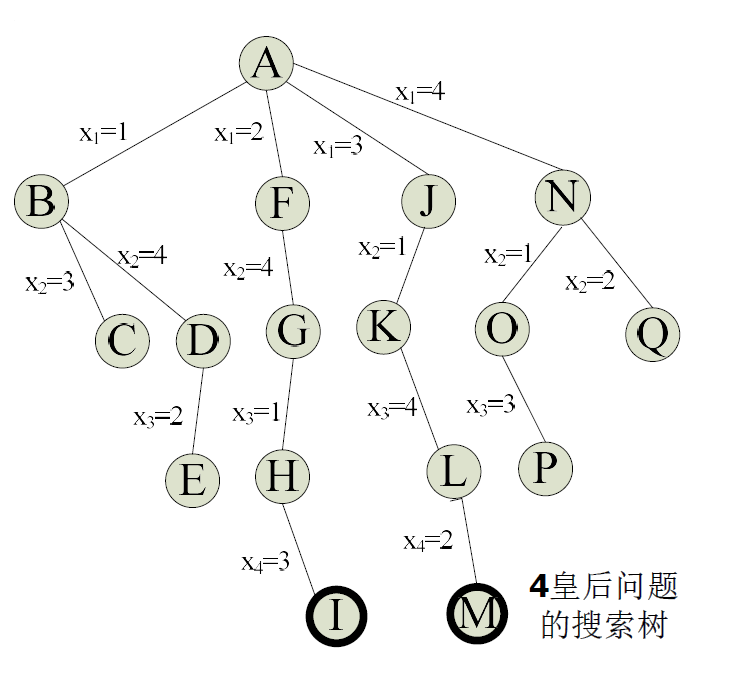
n后问题
解空间树:满m叉树
伪代码
时间复杂度
\(T(n)=O(n^{n+1})\)
空间复杂度
\(S(n)=O(1)\)
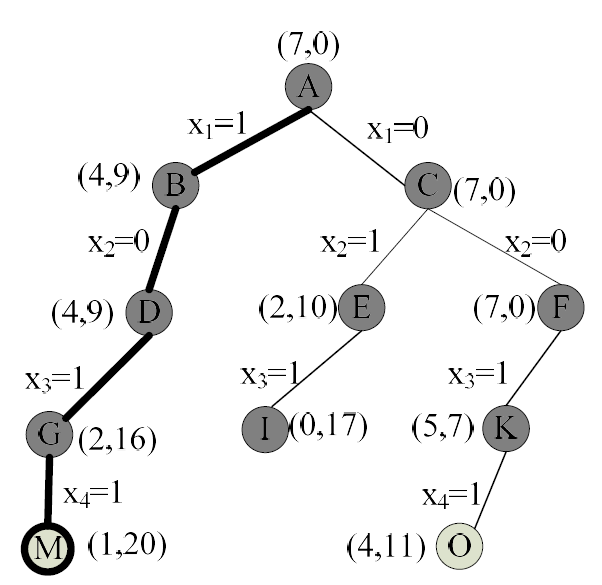
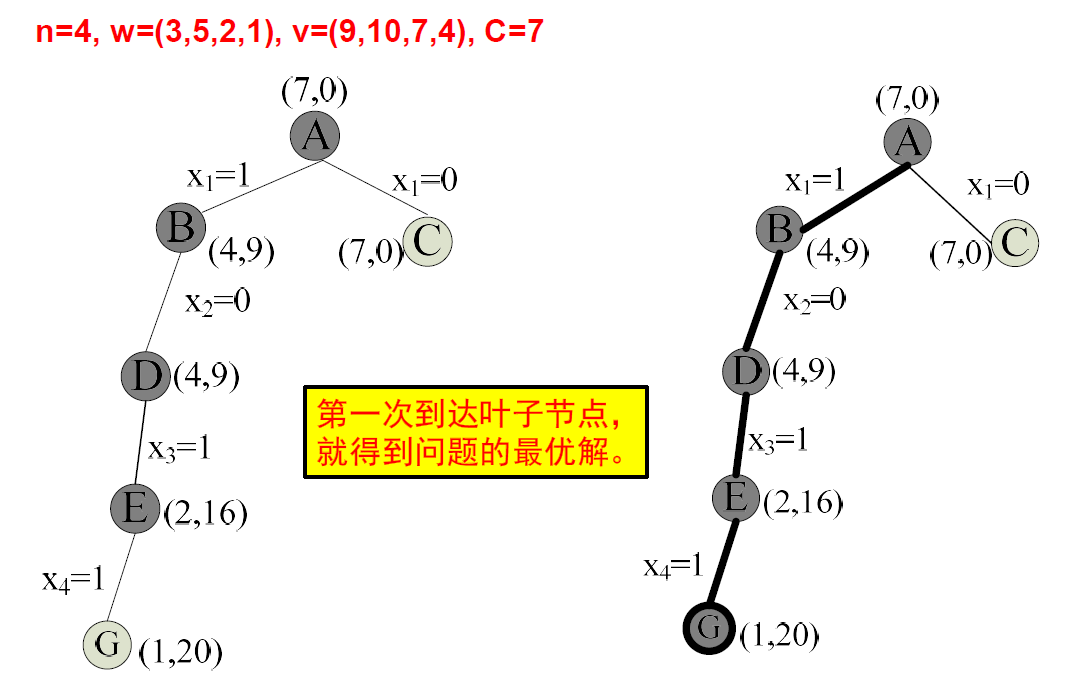
0-1背包问题
子集树
伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Bound(int t, int cp) 输入: Weight数组,Value数组,当前层数t,当前背包装入的总价值cp 输出: cp + rp,即当前背包装入总价值和剩下物品总价值之和 1. for i <- t to N 2. cp <- cp + Value[i] 3. return cp Backtrack_Knapsack_01(int t, int LeftSpace, int cp) 输入: Weight数组,Value数组,当前最优解bestP,当前层数t,当前剩余空间LeftSpace,当前背包装入的总价值cp 输出: Solution_temp数组和Solution数组 1. if t > N //层数大于N,即找到一个解 2. if cp > bestP //如果比当前最优解好,更新解 3. for i <- 1 to N 4. Solution[i] <- Solution_temp[i] 5. bestP <- cp 6. return 7. if LeftSpace >= Weight[t] //搜索左子树,一直搜到底,如果空间够就往里装 8. Solution_temp[t] <- 1 9. cp <- cp + Value[t] //这里可优化掉 10. Backtrack_Knapsack_01(t + 1, LeftSpace - Weight[t], cp) 11. cp <- cp - Value[t] 12. if Bound(t + 1, cp) > bestP //搜索右子树,条件为能找到更优解 13. Solution_temp[t] <- 0 14. Backtrack_Knapsack_01(t + 1, LeftSpace, cp)
bestp在找到一个解后更新
条件为
搜索树:
时间复杂度
空间复杂度
递归栈深度为n,\(O(n)\)
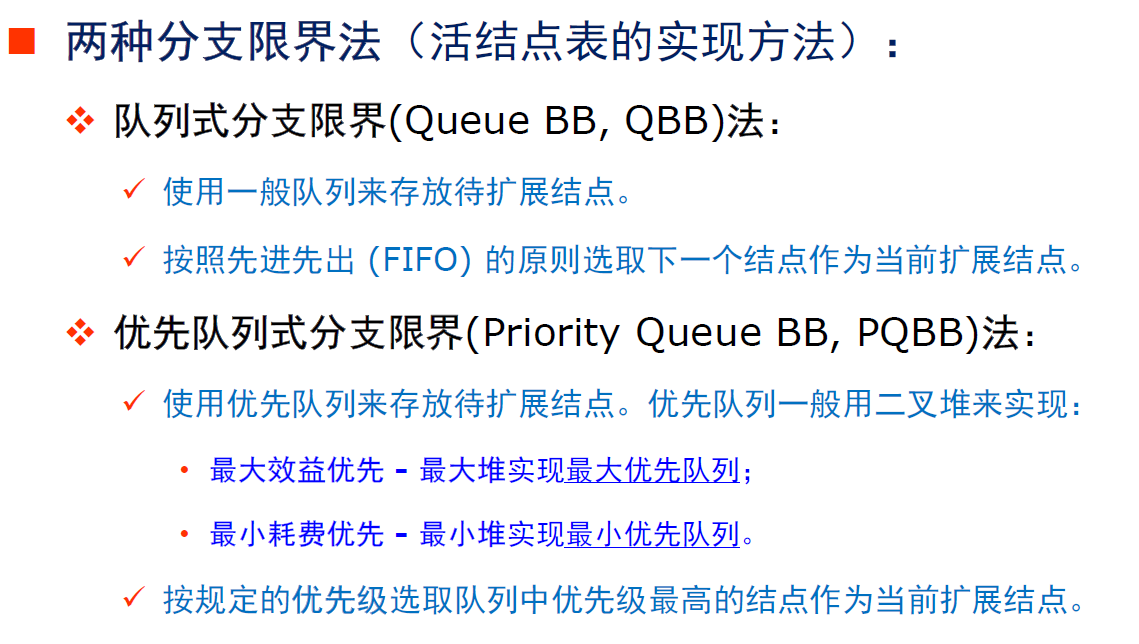
分支限界法
分支限界解题步骤
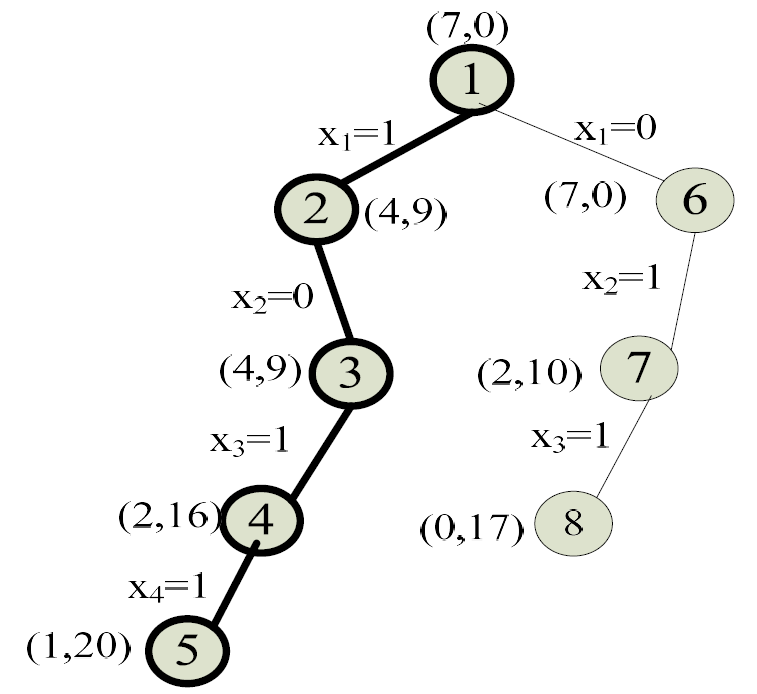
0-1背包问题
brp求法
对剩余物品按单位价值非升排序
如果没装满,就按单位价值装满剩余空间
队列伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Q_BB_Knapsack_01() 输入:Weight数组,Value数组 输出:SolutionIndex是指向最终解的指针 1. bestP <- 0, cp <- 0, leftSpace <- 0, level <- 1 2. SolutionIndex <- NULL 3. que.Enqueue(*(new Node(W, 0, level, -1, NULL))) 4. while !que.isEmpty() 5. temp <- que.Dequeue() 6. level <- temp->level; 7. cp <- temp->TotalValue; 8. leftSpace <- temp->Space; 9. if level > N //层数>N,即找到一个解 10. if cp >= bestP 11. SolutionIndex = temp; 12. continue 13. if leftSpace >= Weight[level] //左子树,有空间就加 14. if cp + Value[level] > bestP 15. bestP <- cp + Value[level] 16. que.Enqueue(*(new Node(leftSpace - Weight[level], cp + Value[level], level + 1, 1, temp))) 17. if Bound(level + 1, cp) > bestP //右子树,满足条件就拓展 18. que.Enqueue(*(new Node(leftSpace, cp, level + 1, 0, temp))) 19. return SolutionIndex
时空复杂度
优先队列伪代码
时空复杂度
概率算法
舍伍德算法
总能求得问题的一个解,且所求得的解总是正确的
降低输入对算法性能的影响,把输入序列打乱,期望得到一个平均的性能
(快排基准元素)
拉斯维加斯算法
可能找不到解,但是找到就是正确的
结合N后问题
蒙特卡洛算法
解未必是正确的
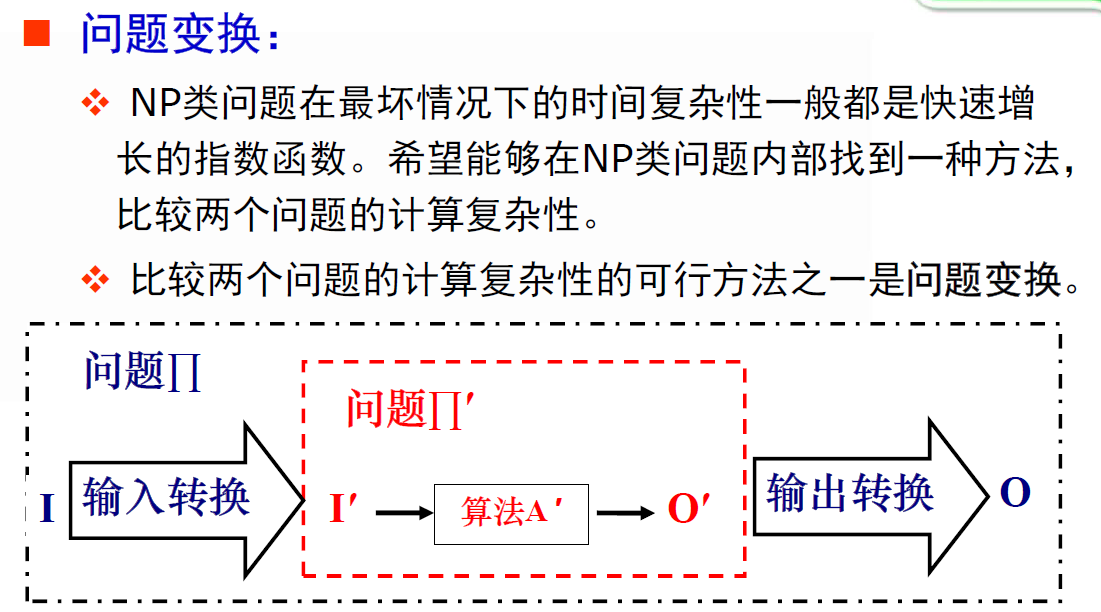
NP完全性理论
掌握概念
易解问题,难解问题
确定性算法,不确定性算法
P类问题,NP类问题
P: Polynomial
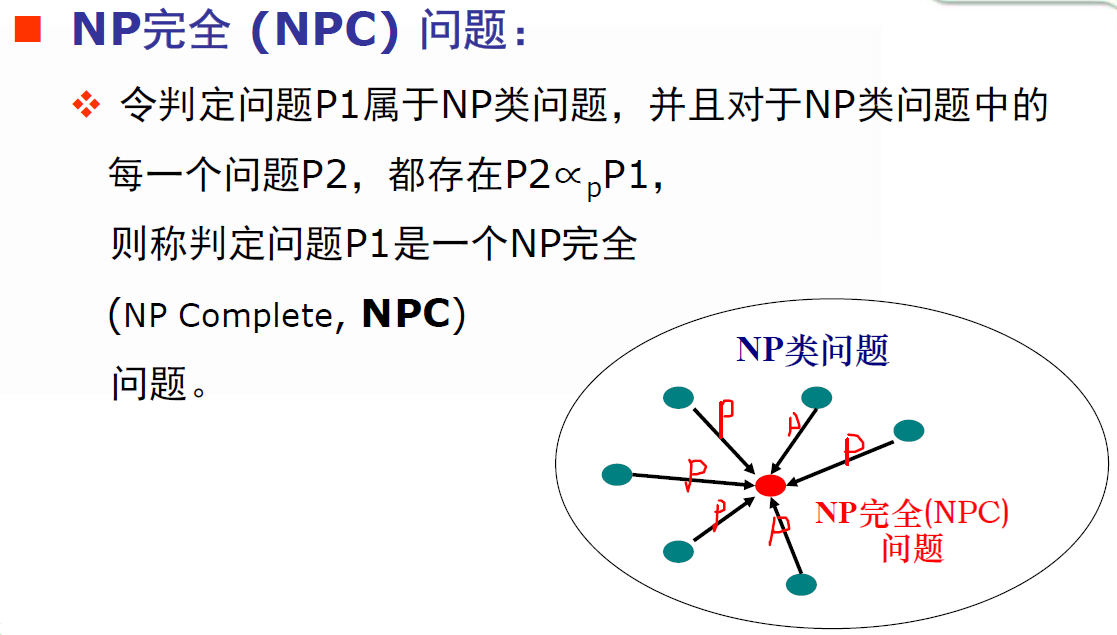
NPC问题
NPC近似解法
串与序列
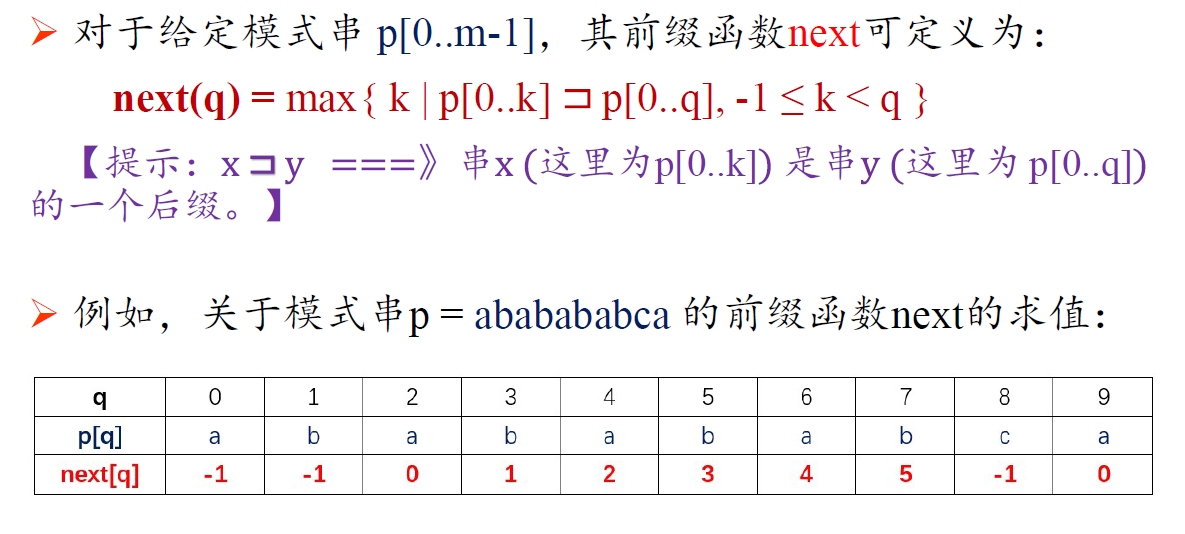
KMP算法
关于“next”数组的定义,我查阅了网上的一些资料,对比了我们学到的内容,发现有些不同
网上对next[i] i从1到n数组的定义是:当出现不匹配时,应该移动模式串,使模式串第i位与主串当前位进行比较
求法:
此处的maxL数组为《算法导论》中定义的π数组:
而我们学到的对next[i] i从0到n-1数组的定义为:
《算法导论》中并没有对next的定义,所以这两种定义可能都是正确的,考试按学的来
学到的next数组求法:下标从0开始,先求出π数组,再每位对应-1
伪代码
求next数组:
时空复杂度
计算next的时间复杂度:\(O(n)\)
参考:
NEXT数列计算
KMP讲解
参考资料
主定理
用主定理解阶乘递归算法的复杂度
归并排序
快速排序
矩阵连乘
最小生成树
NEXT数列计算
KMP讲解
课程PPT