数字信号处理复习整理
数字信号处理复习整理
前言
本次复习整理是针对老师考前串讲内容进行整理,并不是全书所有内容
第一章
什么是消息
消息( Message ):消息是由符号、文字、数字或者语言等组成的序列,一封信、一段文字、新闻
什么是信息
信息( Information ):消息中所包含的事先不确定的内容;信息蕴含在不确定中,不确定内容越多信息量越大;消息是信息的载体;信息论中香农用信息熵来描述信源的不确定度
什么是信号
信号( Signal ):信号是表示消息的物理量,是运载消息的工具,是消息的载体。信号只是消息的一种物理表现形式(比如用声、光、电等);信号较之信息的其他表示形式(文字、语言等),更便于被系统接受和处理
信号通常是一个自变量或多个自变量的函数。如果仅有一个自变量,则称为一维信号;如果有两个以上的自变量,则称为多维信号
信号描述:时间特性和频域特性
信号分类:连续时间信号,离散时间信号
消息,信息,信号之间的联系
信号是消息的表现形式与传送载体
消息是信号的传送内容
信息是人们从消息中得到的、以前不知道的事情、知识等
什么是模拟信号
模拟信号:时间和幅值均为连续的信号
什么是采样信号
离散信号:时间是离散的,幅值是连续的信号
什么是数字信号
数字信号:时间和幅值均为离散的信号
模拟信号、采样信号、数字信号如何转换
模拟信号抽样得到离散信号,离散信号量化得到数字信号
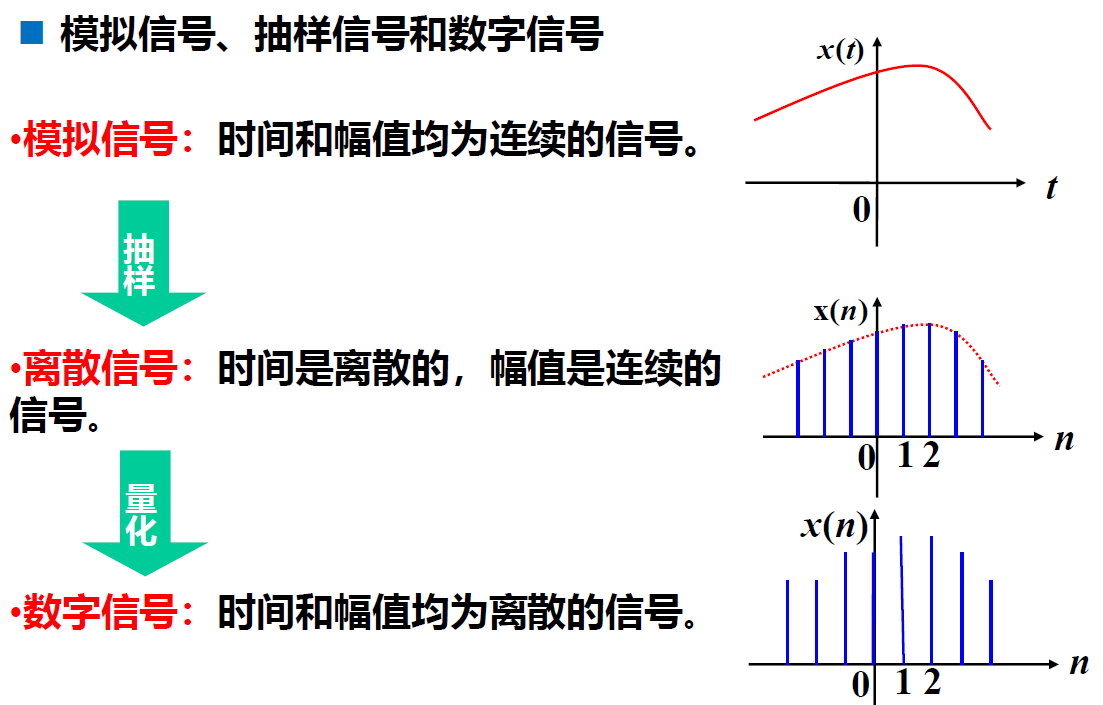
序列的运算
加法和乘法
乘法和加法:序列之间的乘法和加法是指它的同序号的序列值逐项对应相乘(点乘)和相加
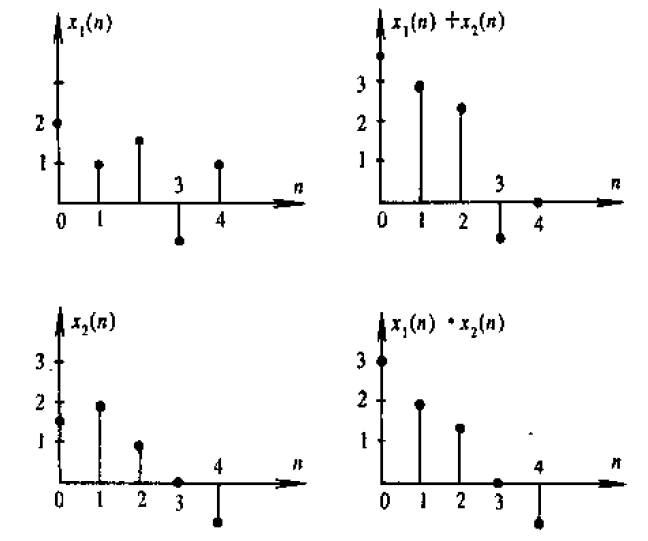
平移
将序列\(x(n)\)沿\(n\)轴向前平移\(n_0\),得到信号\(x(n-n_0)\)
当\(n_0>0\)时,为\(x(n)\)的延时序列
当\(n_0<0\)时,为\(x(n)\)的超前序列
以0为基准,0之后为未来,还未发生,即“延时”;0之前为已经发生,即“超前”
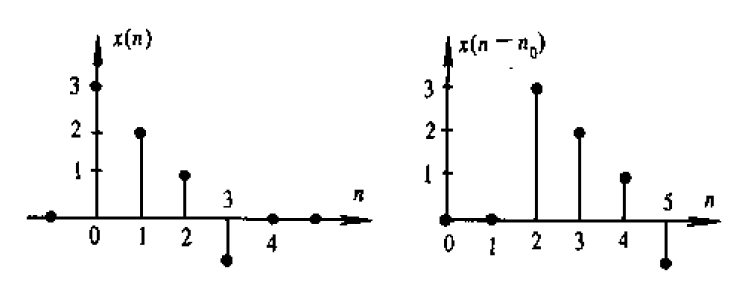
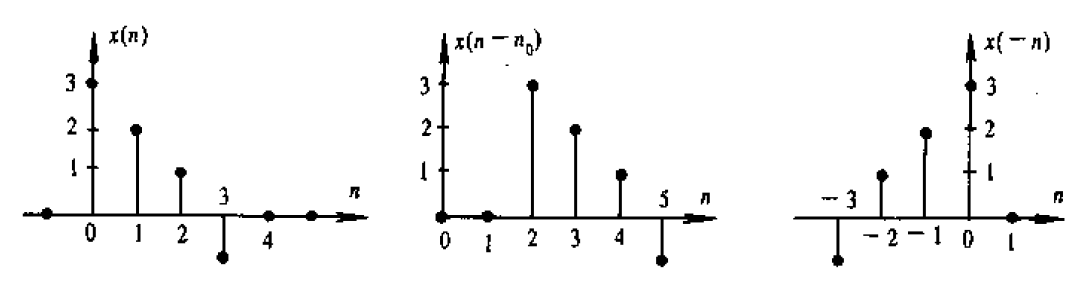
翻转
翻转:沿纵轴进行折叠,将原信号波形翻折180 度;把序列的过去与未来对调\(x(n)\rightarrow x(-n)\);也称为信号的反叠
尺度变换
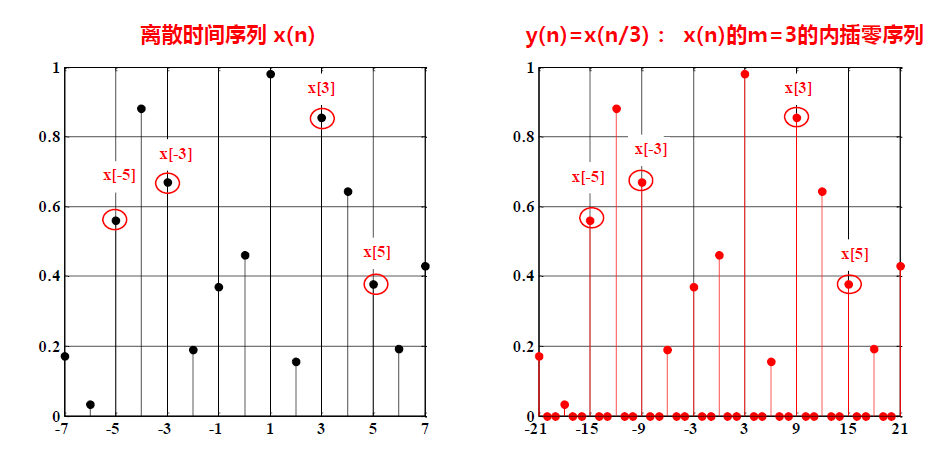
尺度变换:\(x(nm)\rightarrow x(n)\):
对原序列进行抽取(\(m>1\))或插0(\(m<1\))
抽取(m>1)
\(x(nm)\rightarrow x(n),\qquad m>1\)
改变后的新序列是\(x(nm)\)
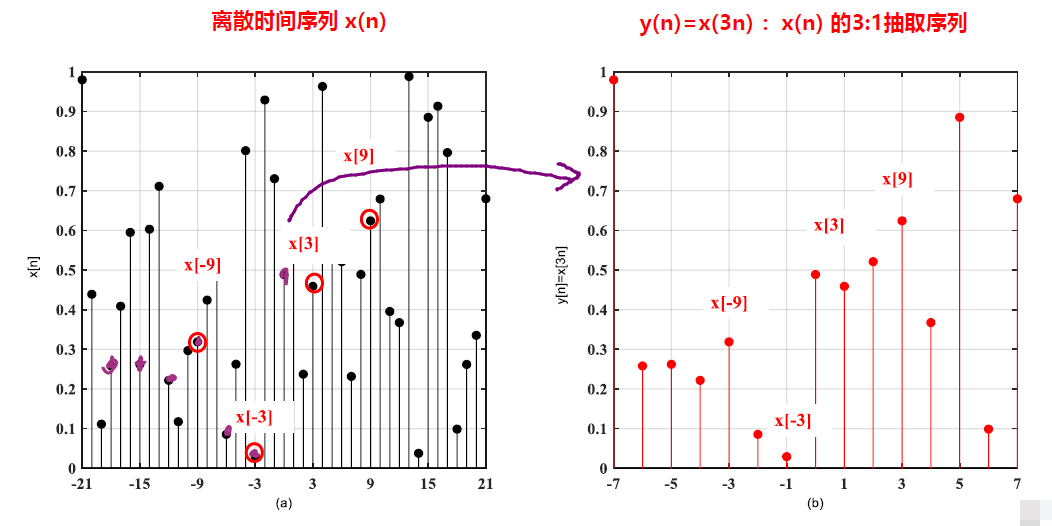
插值(m<1)
\(x(nm)\rightarrow x(n),\qquad m<1\)
改变后的新序列是\(x(nm)\)
原序列相邻序列值之间插入\(\dfrac{1}{m}-1\)个0
如图,\(m=\dfrac{1}{3}\),插入2个0
典型序列
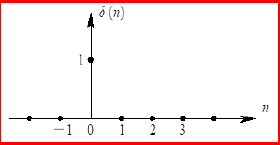
单位脉冲(采样)序列\(\delta(n)\)
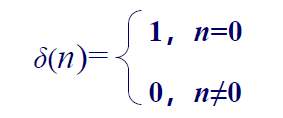
单位脉冲序列也可以称为单位采样序列,特点是仅在n=0时取值为1,其它均为零
对于任意序列,可采用单位脉冲序列的移位加权和表示
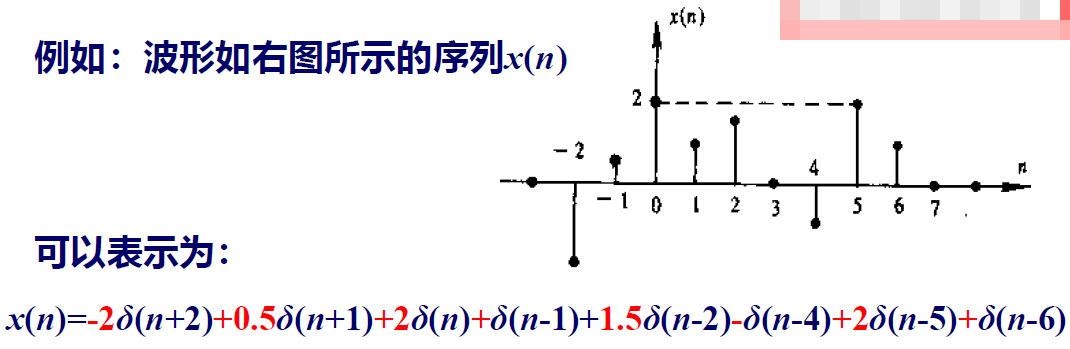
单位阶跃序列\(u(n)\)
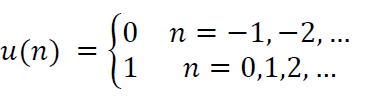
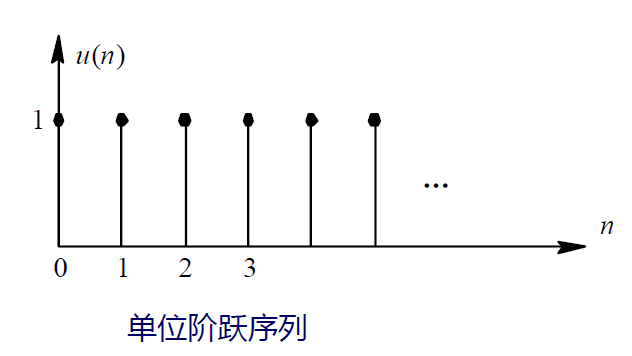
矩形序列\(R_N(n)\)
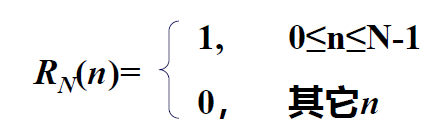
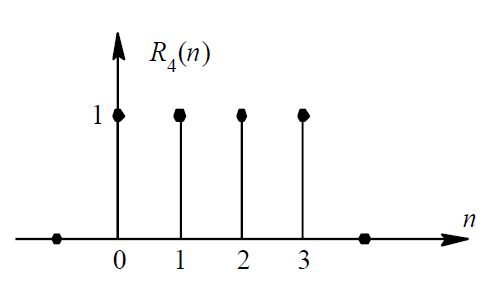
N为矩形序列长度,如图,N为4
矩形序列可用单位阶跃序列表示为:\(R_N(n)=u(n)-u(n-N)\)
复指数序列

线性系统
同时满足可加性和齐次性

例题

时不变系统(没强调)

零输入响应
零输入响应:没有外加激励信号的作用,只由起始状态作用(起始时刻系统储能)而产生的响应
对应模电里电容元件放电
零状态响应
零状态响应:不考虑原始时刻系统储能的作用(起始状态(n<0)时系统状态等于零),由系统的外加激励信号产生的响应
对应模电里电容元件充电

线性卷积
卷积的物理意义

线性卷积如何计算

例题
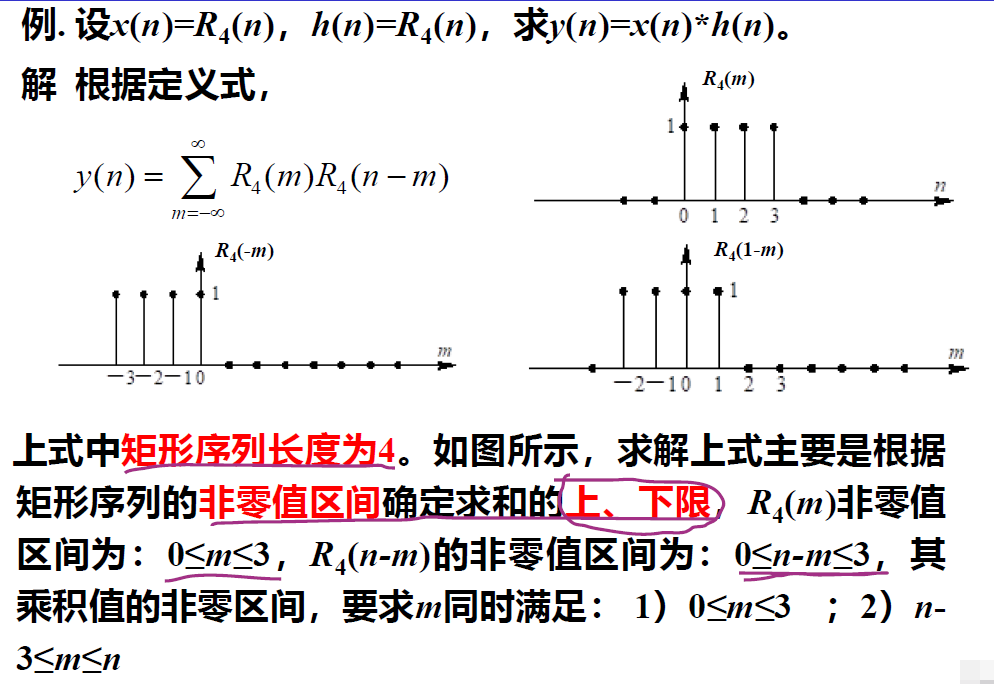
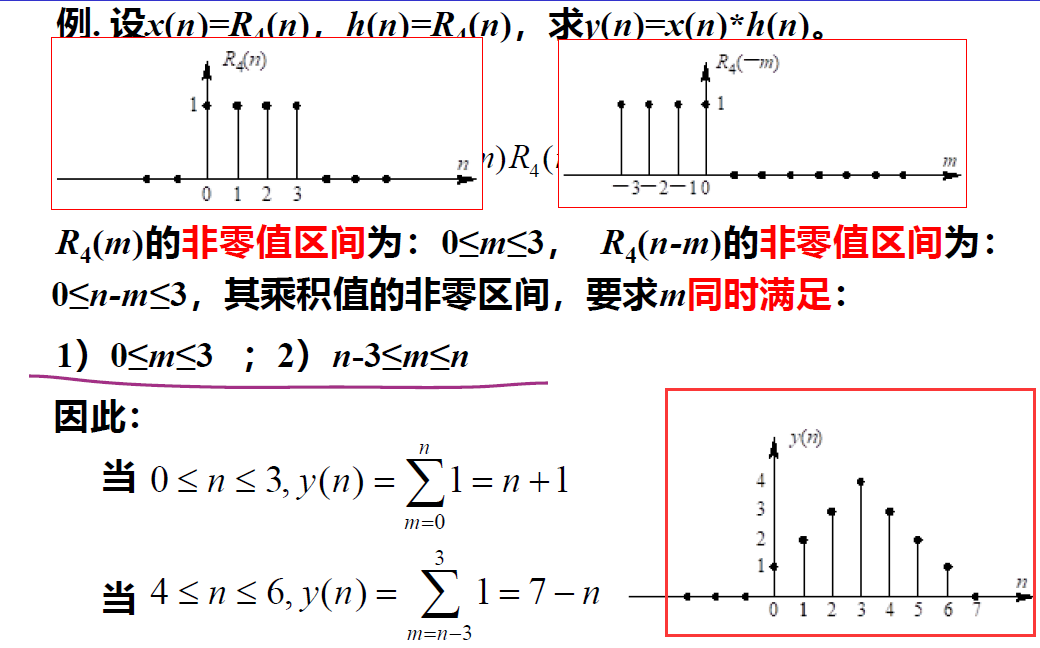
简单方法:
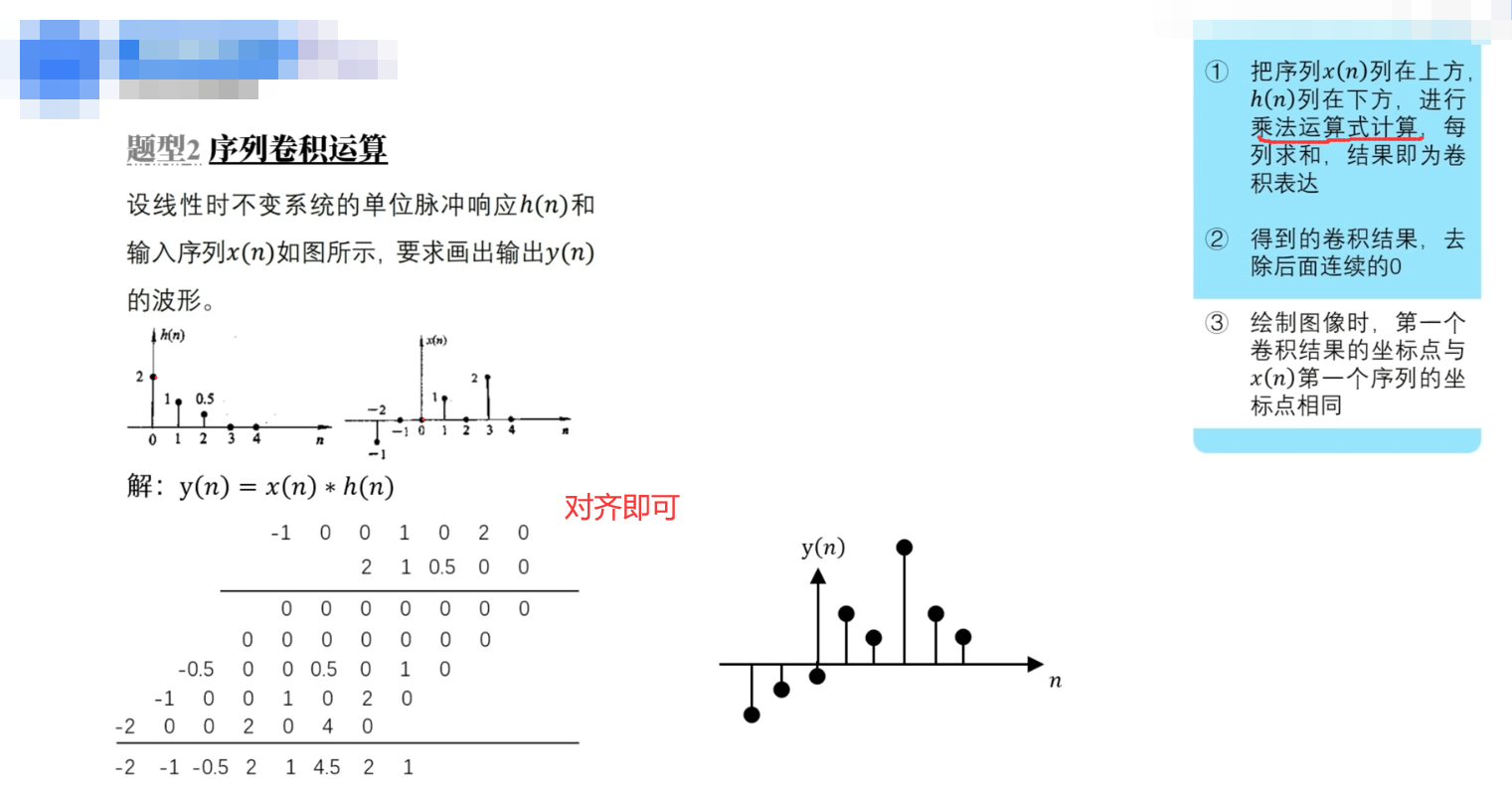
参考:序列卷积计算方法
作业

(1)
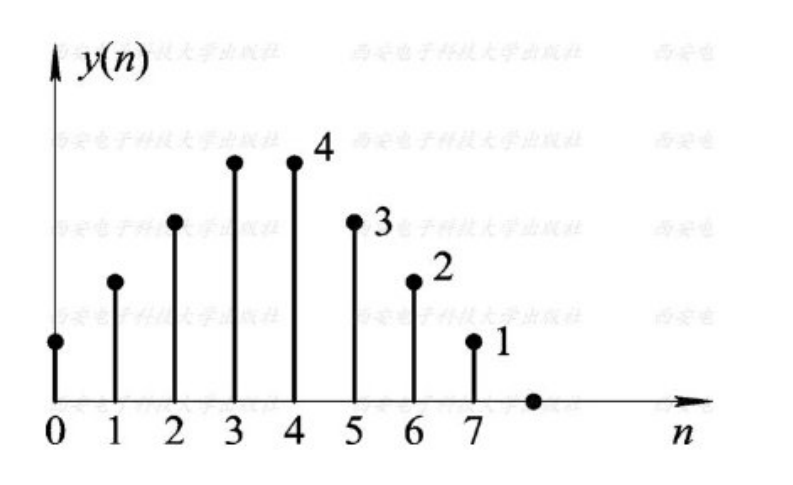
(2)
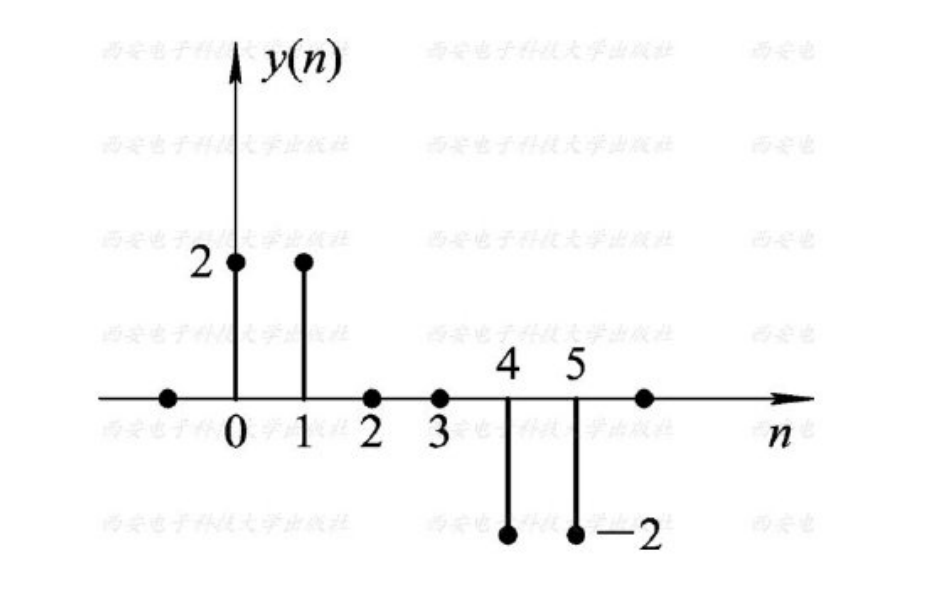
线性卷积性质

即线性卷积服从交换律、结合律、分配律
序列本身与单位脉冲序列的卷积和等于序列本身:

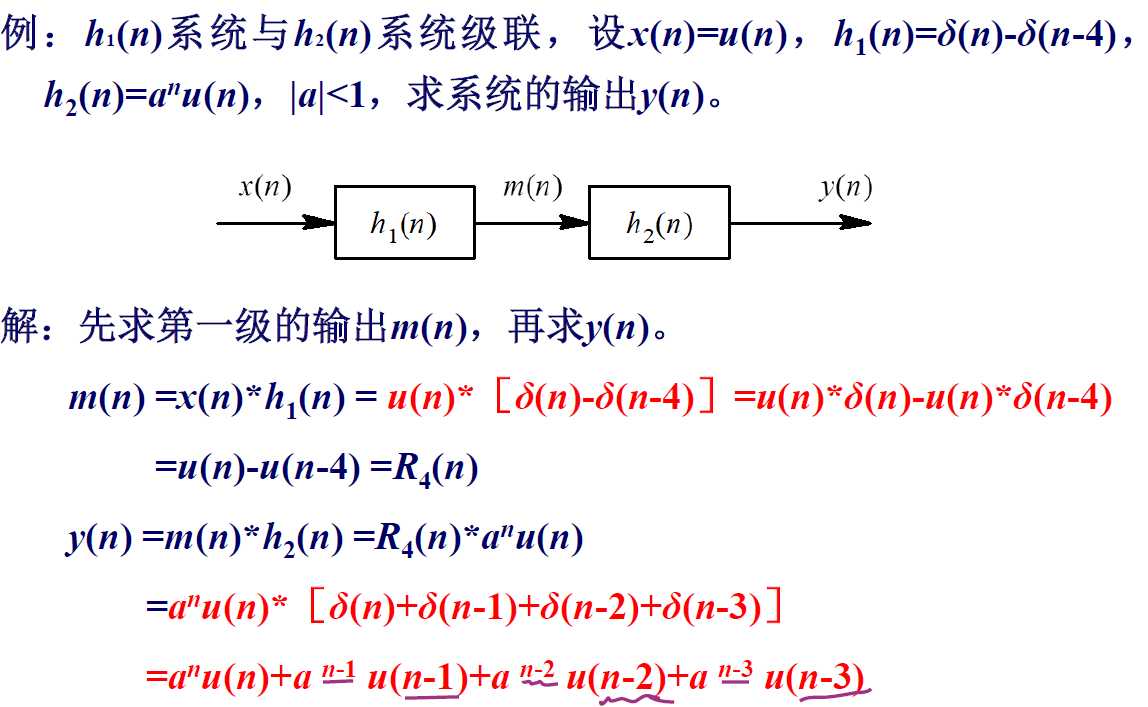
例题
因果性稳定性
系统的因果性
如果系统n时刻的输出,只取决于n时刻以及n时刻以前的输入序列,而和n时刻以后的输入序列无关,则称该系统具有因果性质,或称该系统为因果系统
如果n时刻的输出还取决于n时刻以后的输入序列,在时间上违背了因果性,系统无法实现,则系统被称为非因果系统。因此系统的因果性是指系统的可实现性
线性时不变系统具有因果性的充分必要条件是系统的单位取样响应满足下式:\(h(n)=0,\quad n<0\)
系统的稳定性
所谓稳定系统,是指如果系统输入是有界的,系统输出也是有界的
系统稳定的充分必要条件是系统的单位取样响应绝对可和:\(\sum\limits^\infty_{n=-\infty}|h(n)|<\infty\)
分析系统是否因果稳定
差分方程形式一般都靠假设
因果就看输出是否与n时刻以后的输入无关
稳定就看是否收敛
例题:给定y(n)或h(n)判断因果稳定
设\(y(n)=e^{x(n)}\),试分析该系统因果稳定性
因为y(n)只与x(n)有关,与n时刻以后的输入无关,该系统为因果系统
稳定性证明:


作业:给定差分方程判断因果稳定



PPT 2.6节
用系统函数的极点分布分析因果稳定
因果:系统函数\(H(z)\)的收敛域包括\(\infty\)点
稳定:系统函数\(H(z)\)的收敛域包括单位圆(\(|z|=1\))
例题:给定系统函数分析因果稳定

第二章
DTFT

等比数列求和公式:\(S_n=a_1\cdot\dfrac{1-q^n}{1-q}\)
欧拉公式:\(e^{j\theta}=\cos\theta+j\sin\theta\)
DTFT计算例题
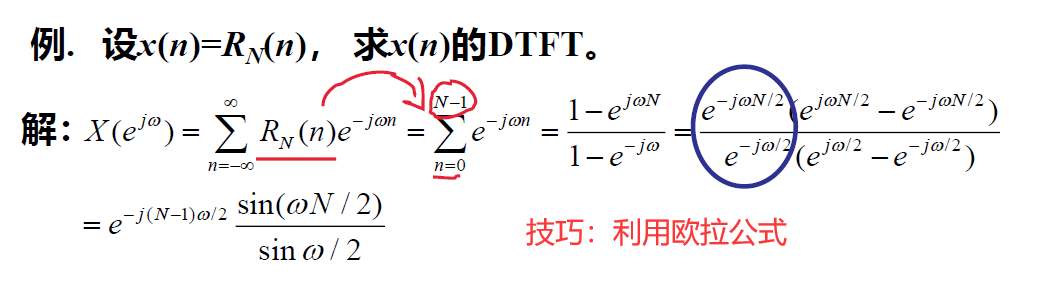
技巧:出现\(1-e^{指数}\),提出来的都是\(e^{负\dfrac{|指数|}{2}}\),然后利用欧拉公式,注意计算
DTFT性质
线性

时移与频移
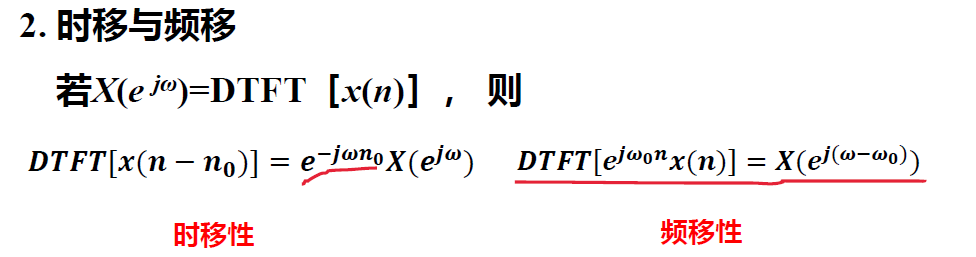
时移证明:

频移证明:
对称性
共轭:\((e^{j\theta})^*=e^{-j\theta}\)
\[ \begin{align*} e^{j\theta}&=\cos\theta+j\sin\theta\\\\ (e^{j\theta})^*&=\cos\theta-j\sin\theta\\ &=\cos\theta+j\sin(-\theta)\\ &=\cos(-\theta)+j\sin(-\theta)\\ (e^{j\theta})^*&=e^{-j\theta} \end{align*} \]




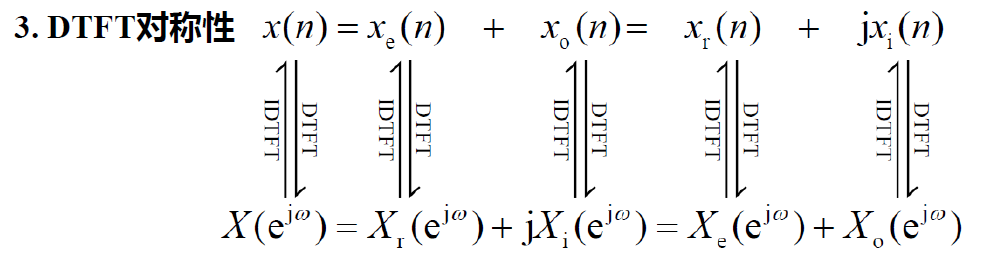
时域卷积定理
时域卷积=频域乘积
令\(k=n-m\)

频域卷积定理
\(时域乘积=\dfrac{1}{2\pi}频域卷积\)

帕斯维尔定理
性质:\(x(n)\cdot x(n)^*=|x(n)|^2\)

Z变换


Z变换有收敛域


Z变换计算例题


分类讨论:

Z变换性质
线性

序列移位
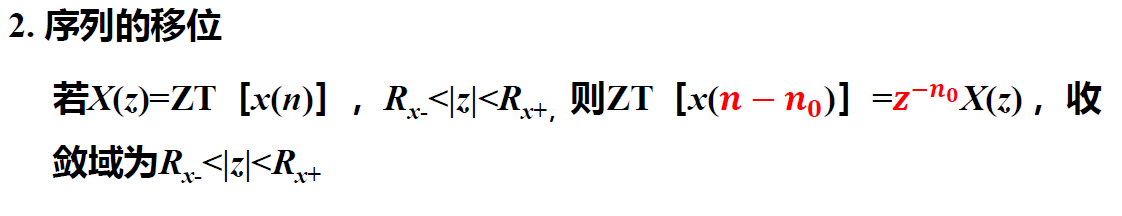
乘指数序列
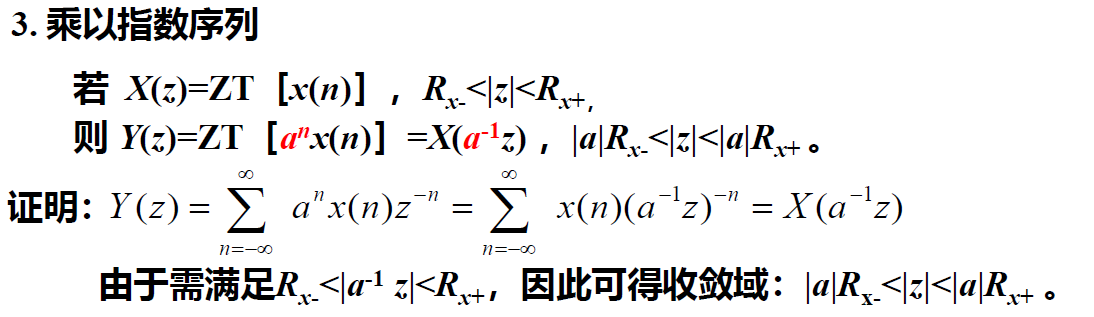
序列乘n
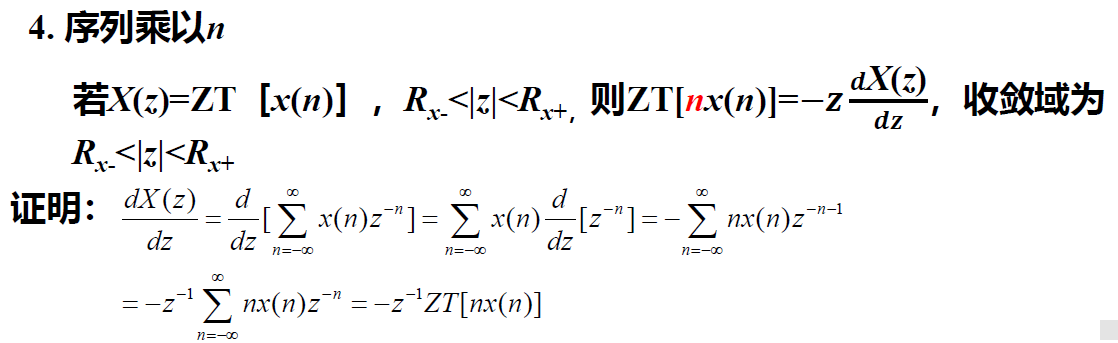
初值定理
序列卷积和

作业
给定变换后求对应式的DTFT

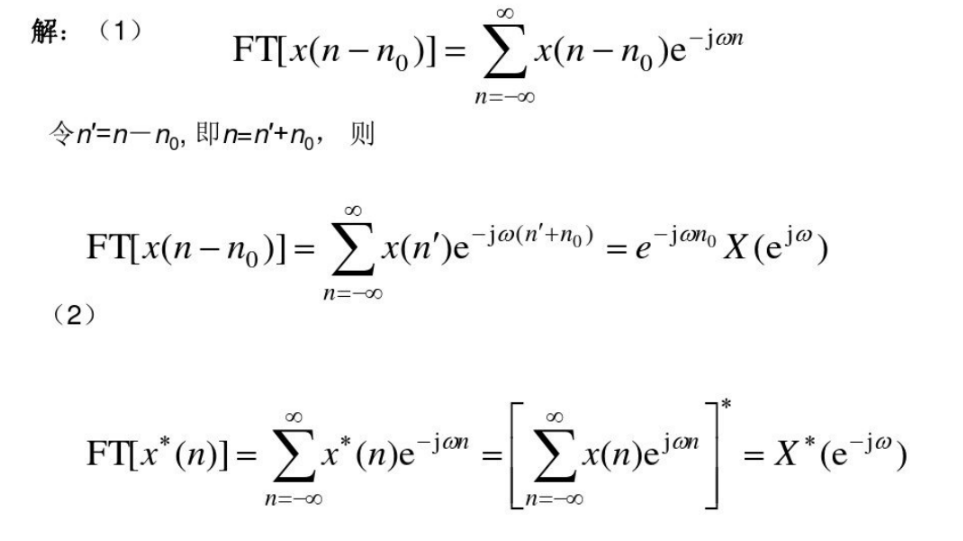

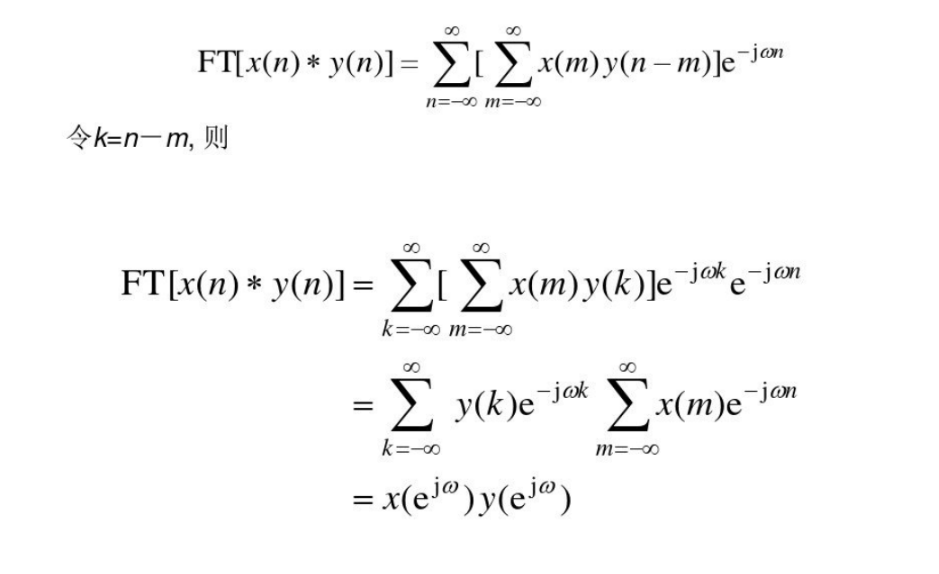
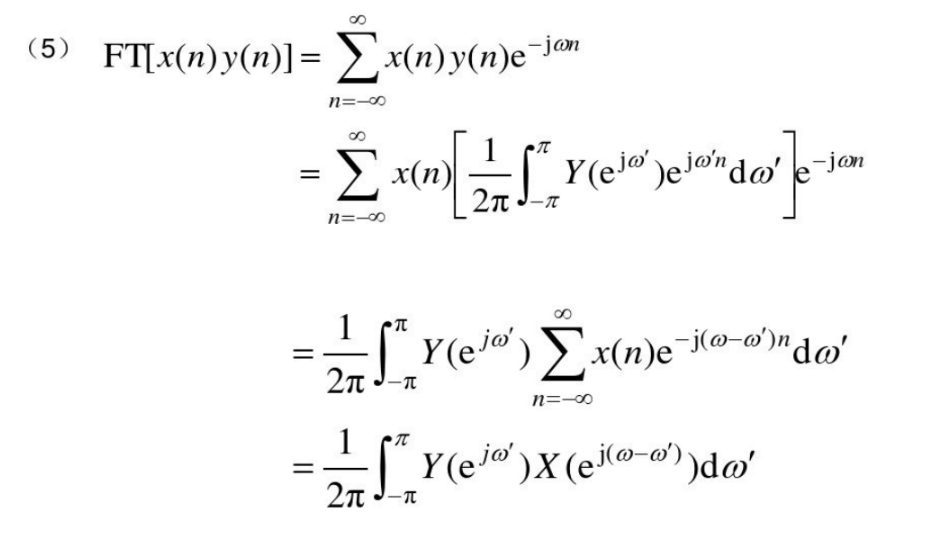

给定原序列求DTFT
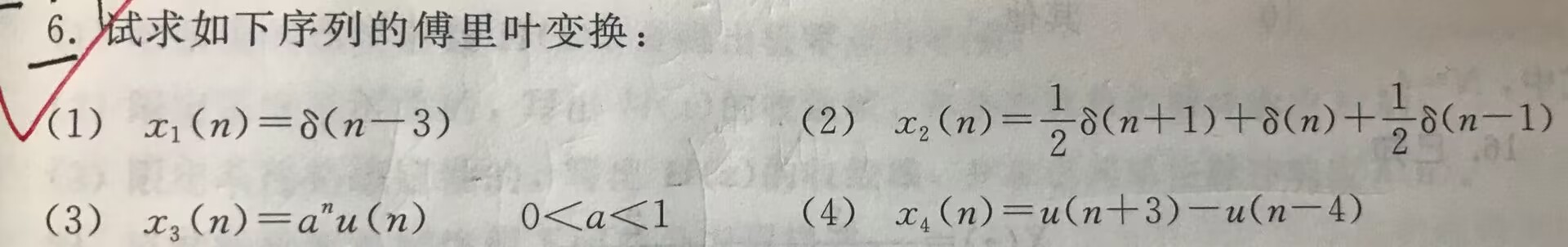
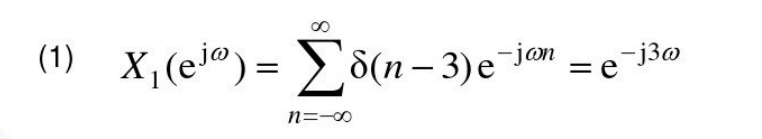
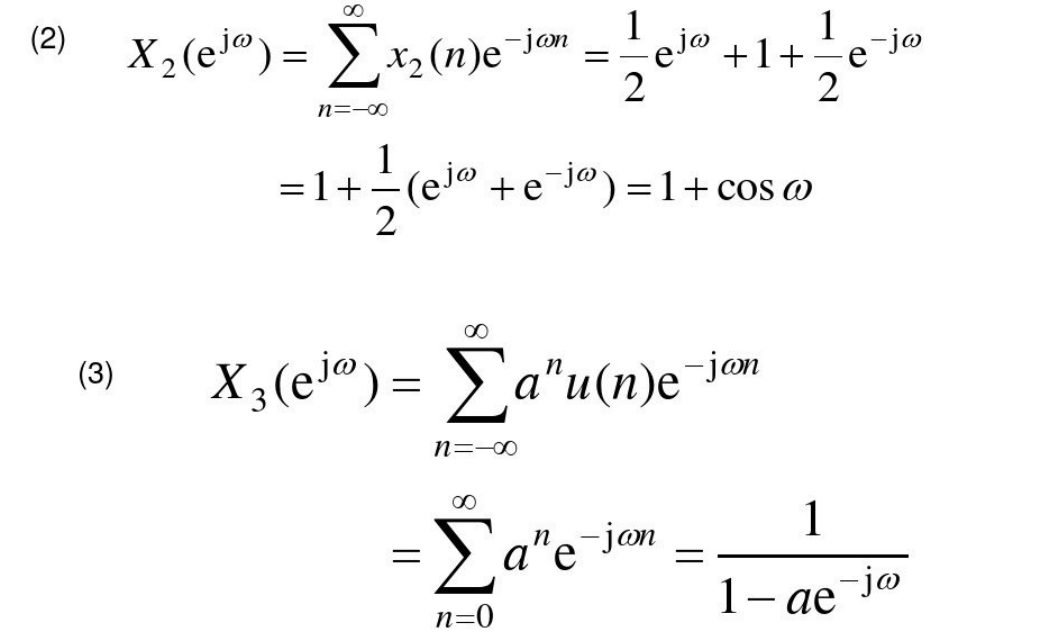

给定原序列求Z变换及收敛域

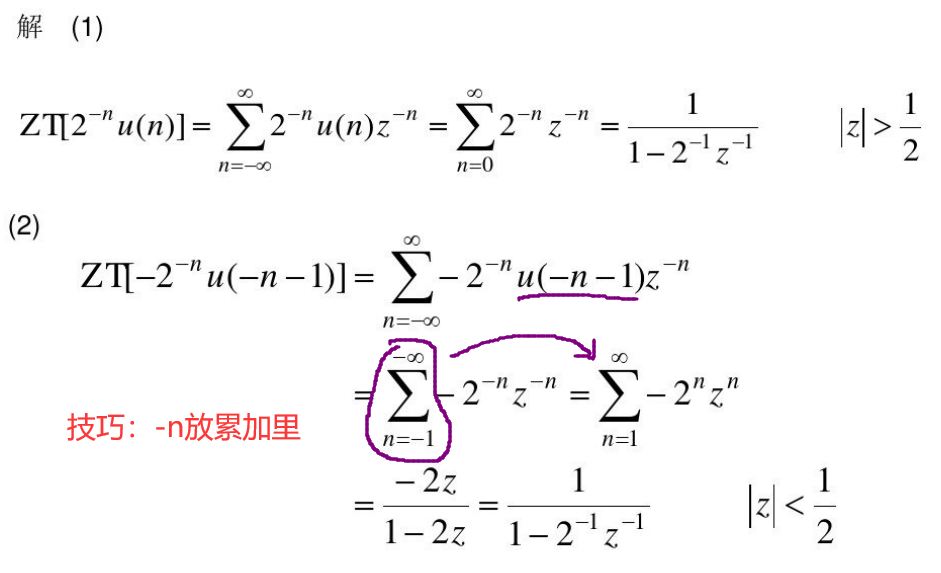
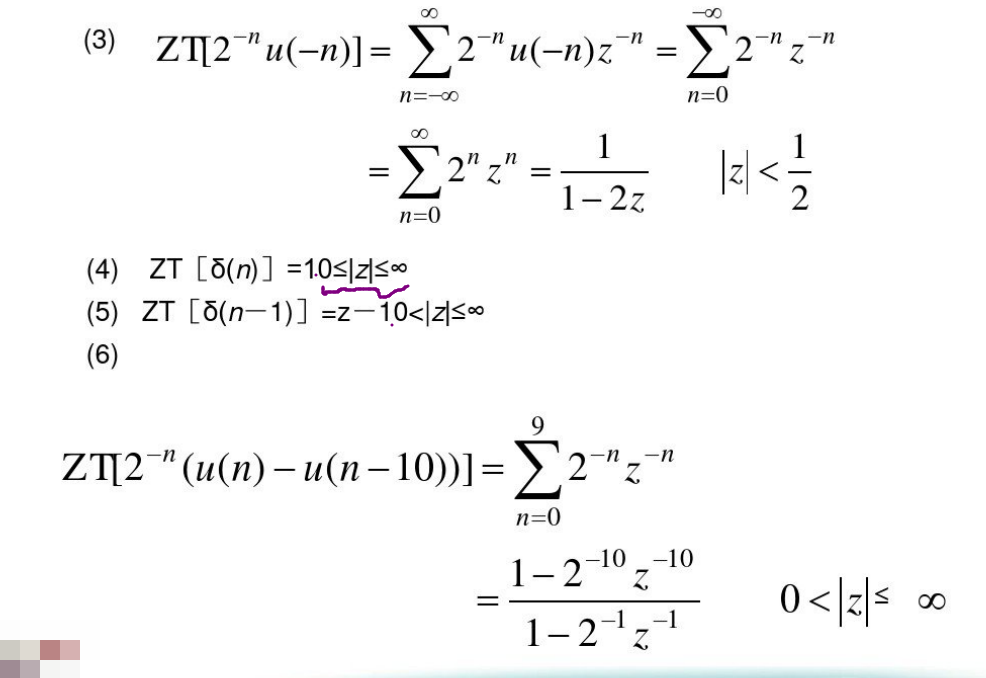
第三章
DFT

物理意义
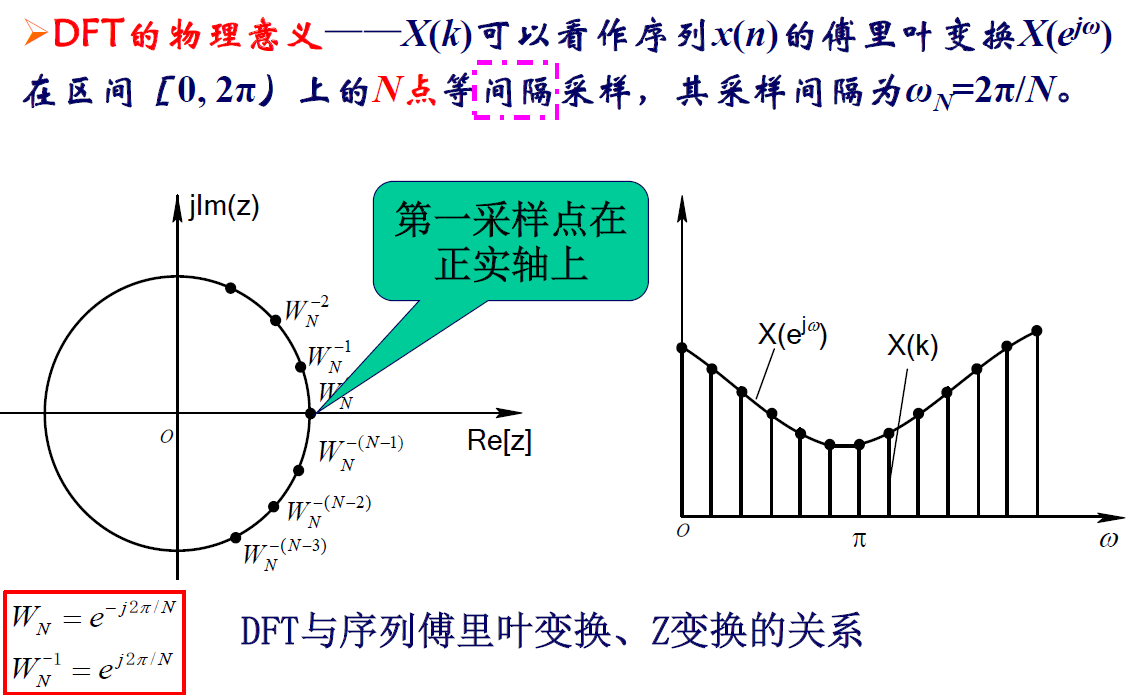
例题

常规题:给出明确的序列
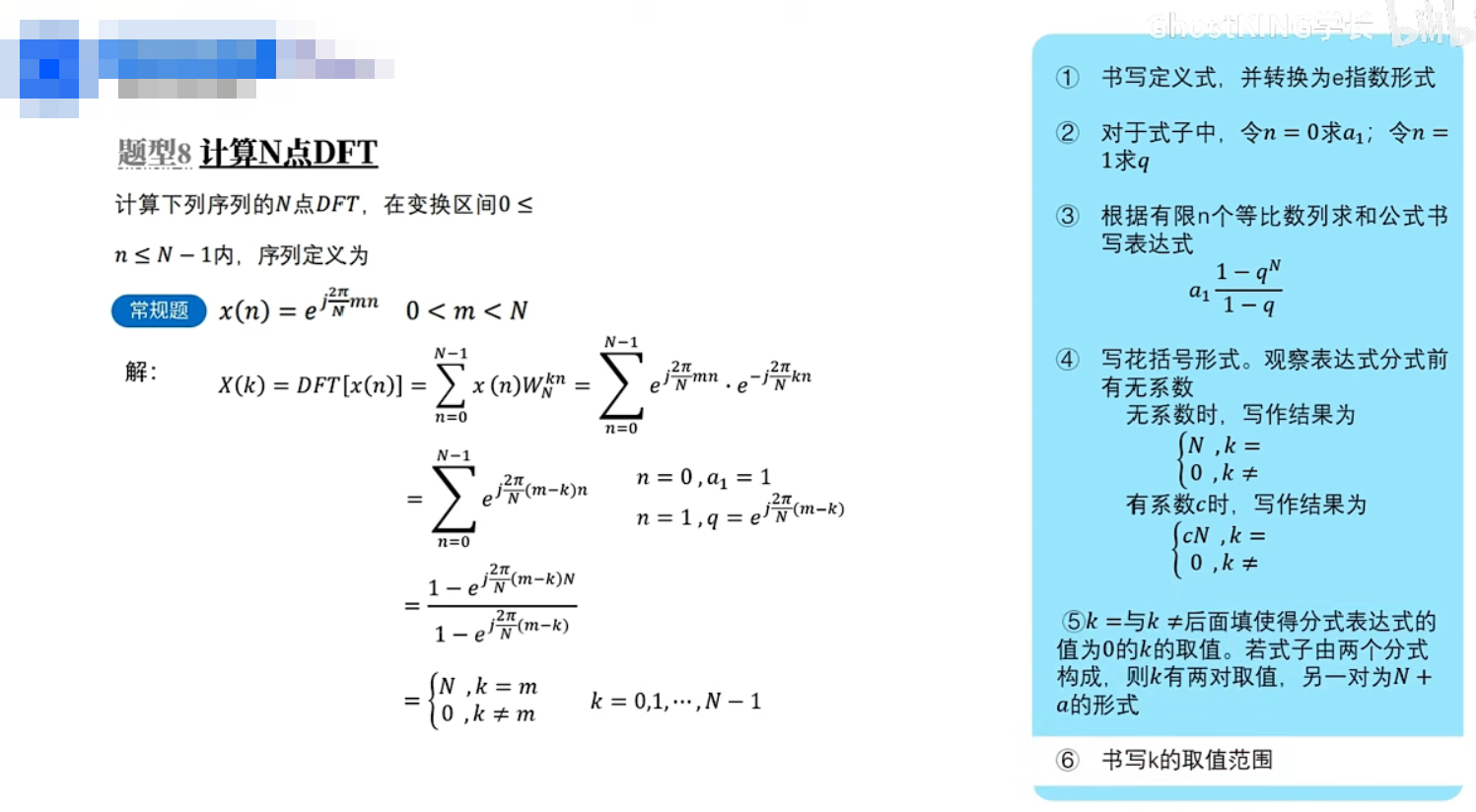

特殊题:序列为\(R_m(n)\)

循环卷积

作业
求序列DFT
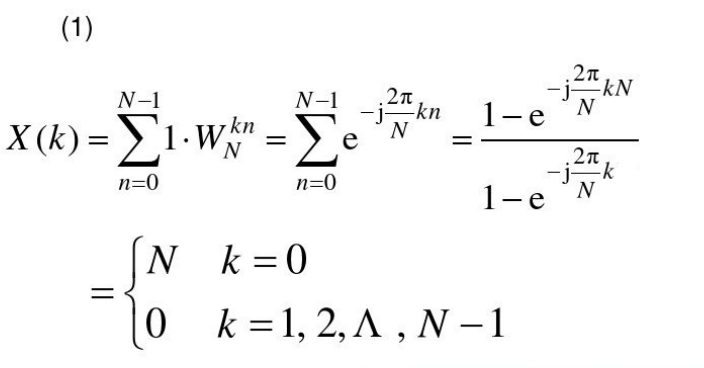
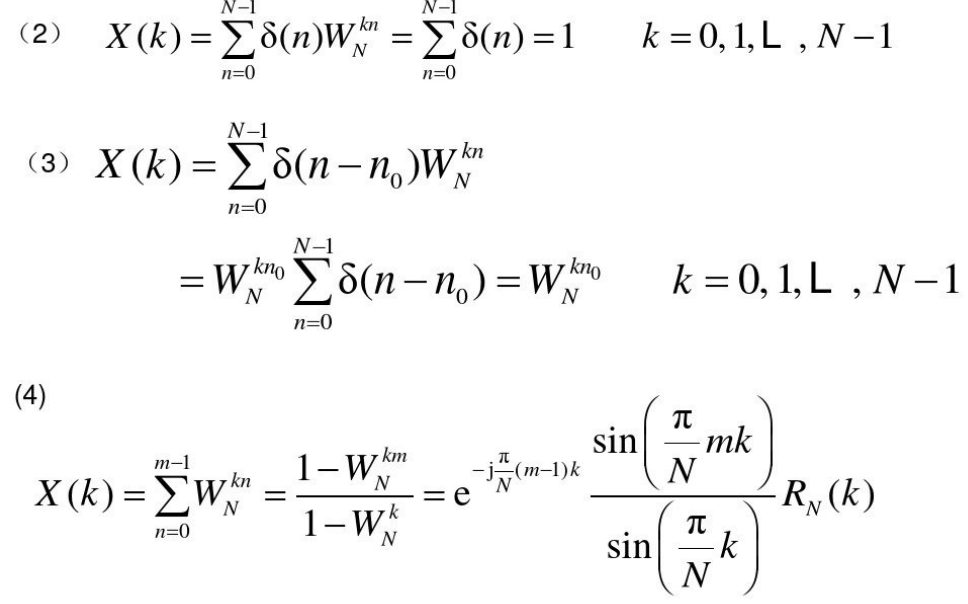
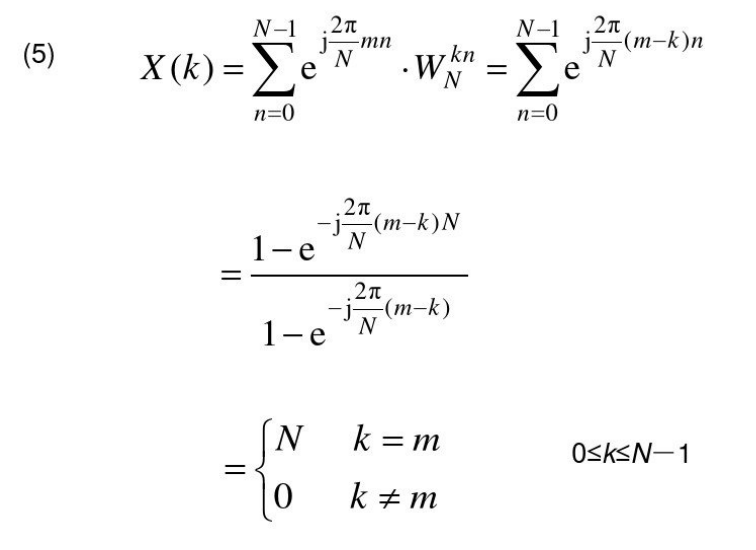
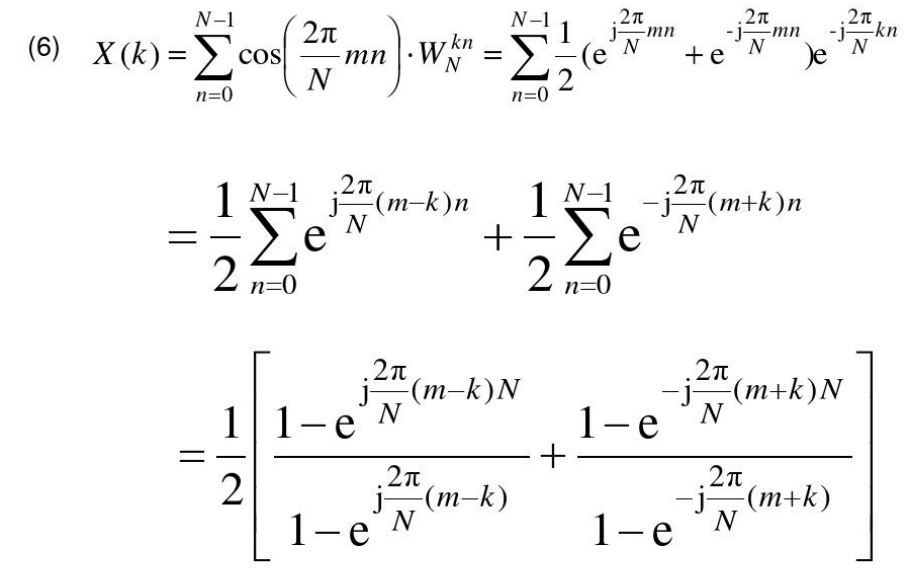

求IDFT
注:\(e^{2\pi n}=1\)
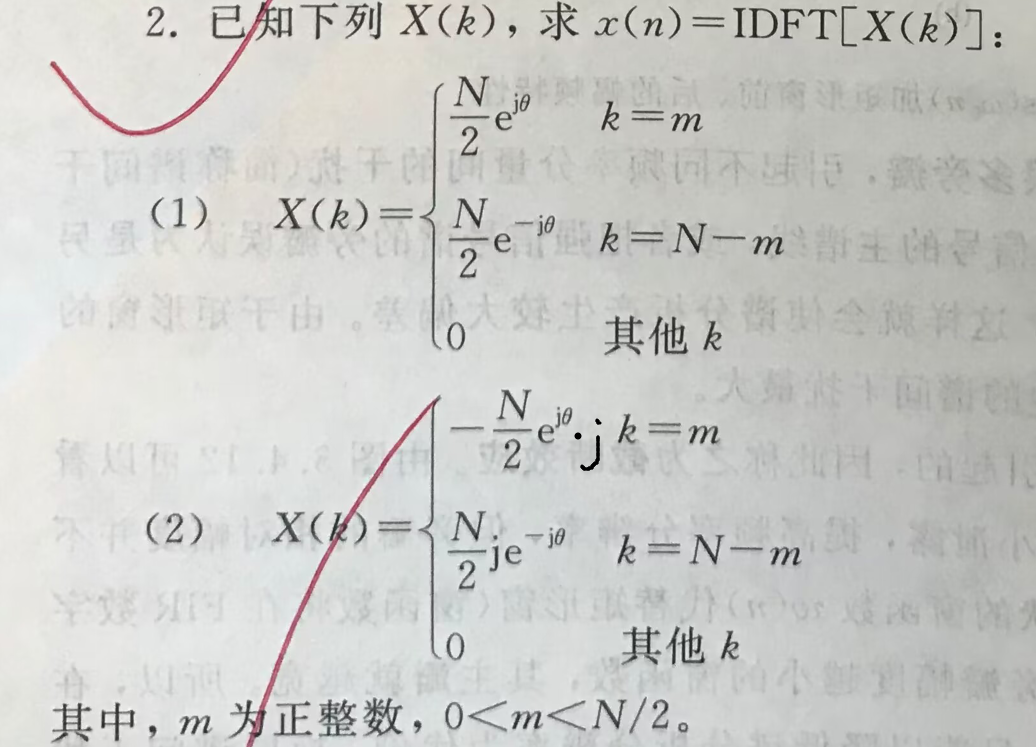
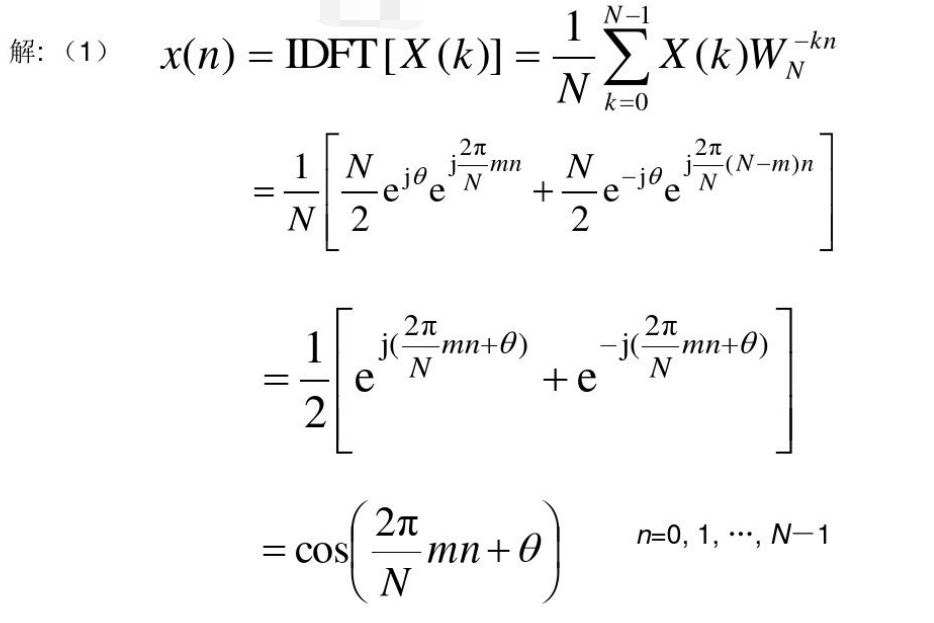
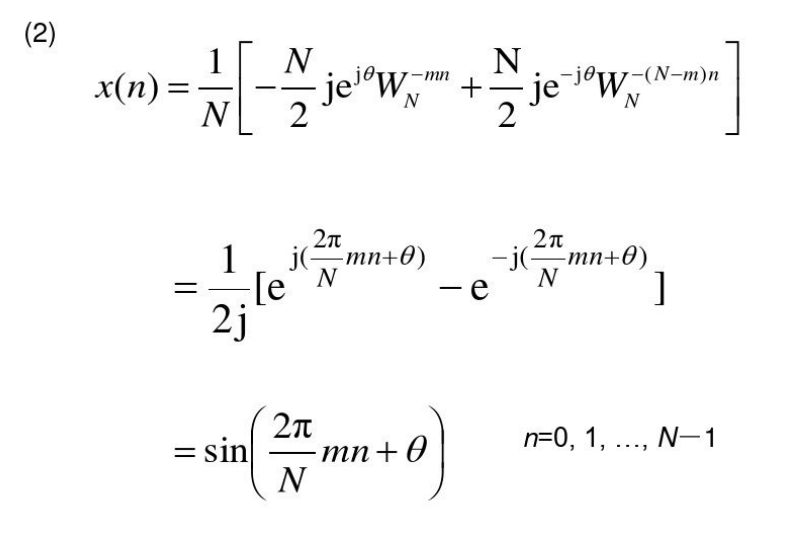
求循环卷积
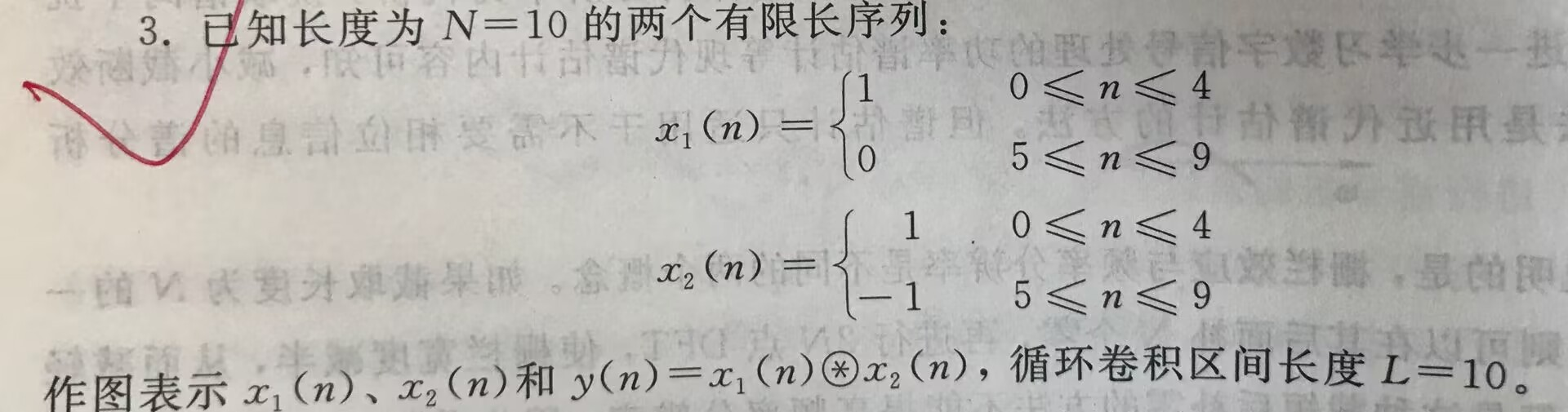

求Y(k)与X(k)关系式
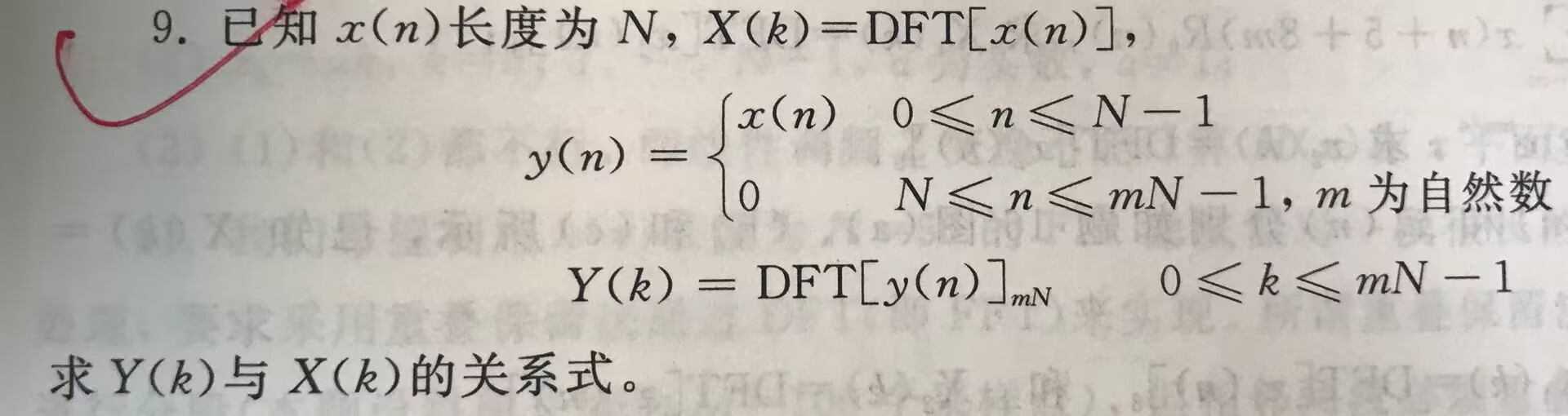
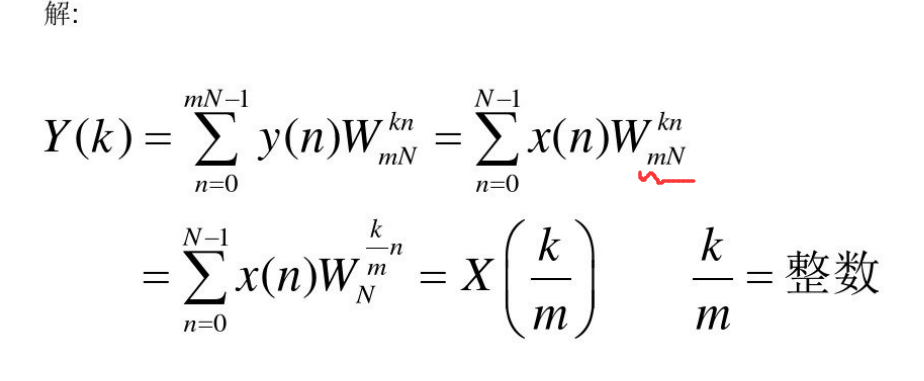

不会
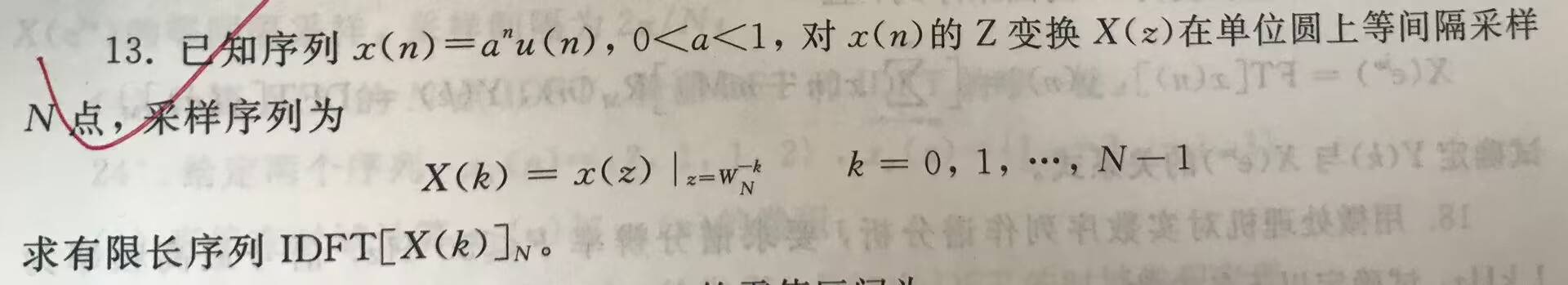


第四章
FFT

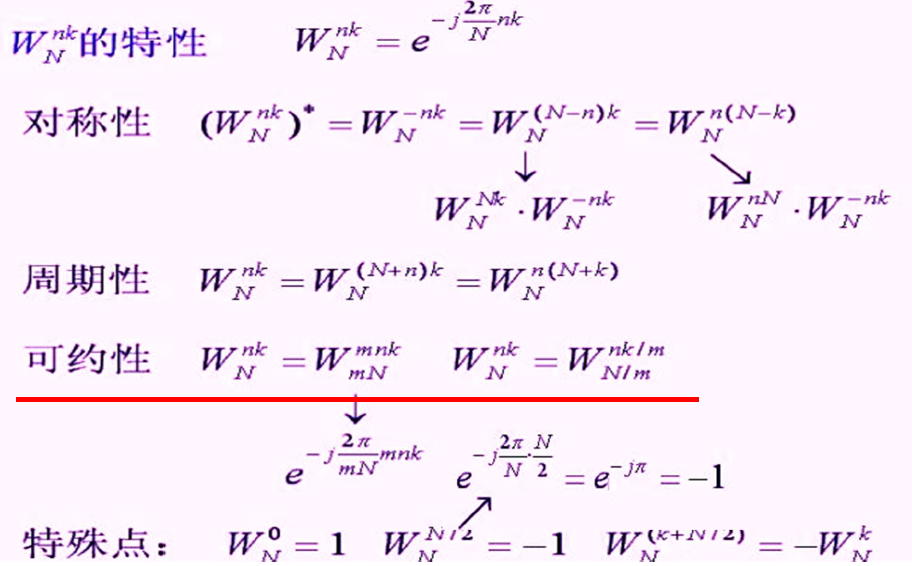
例题

蝶形运算
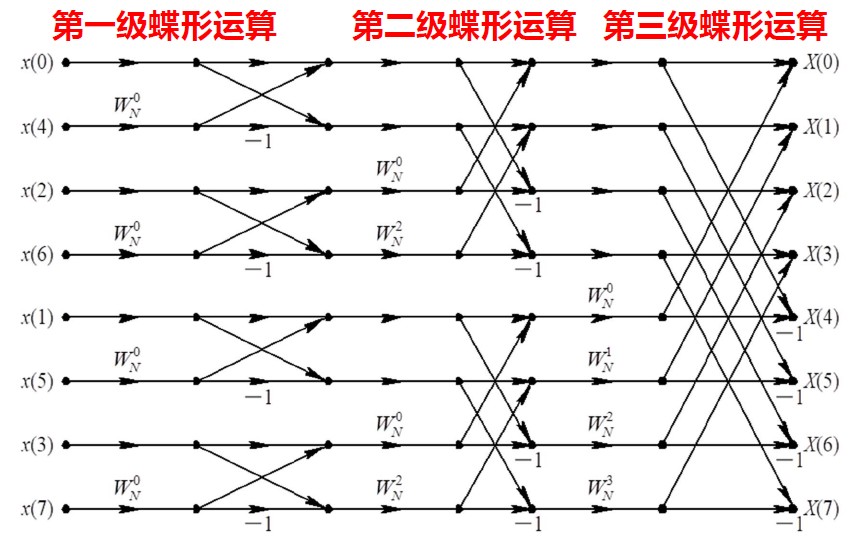
按时间抽取(DIT)的FFT特点
同址运算(原位运算)

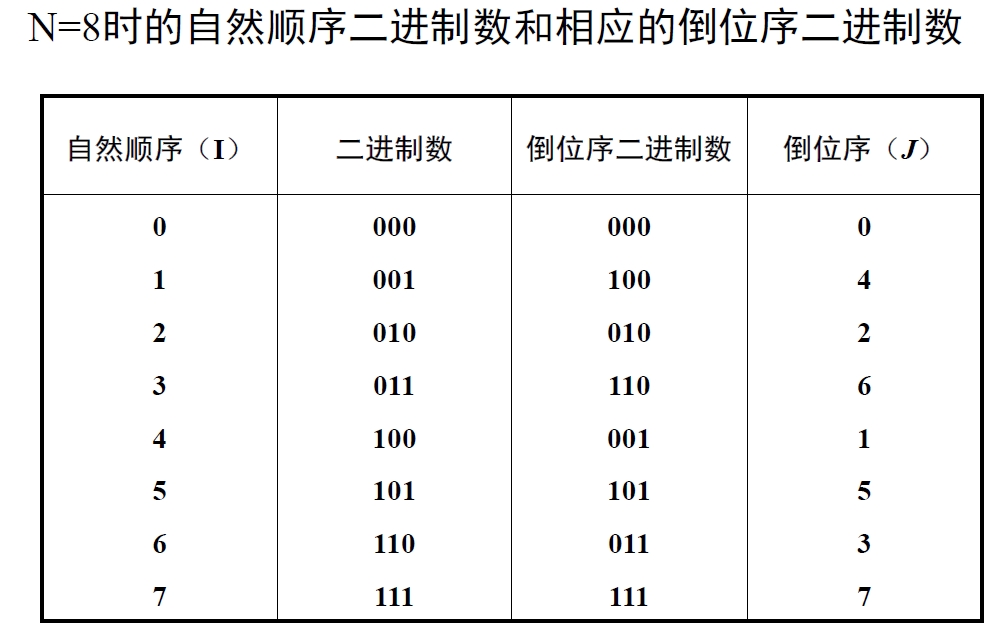
倒位序


第五章
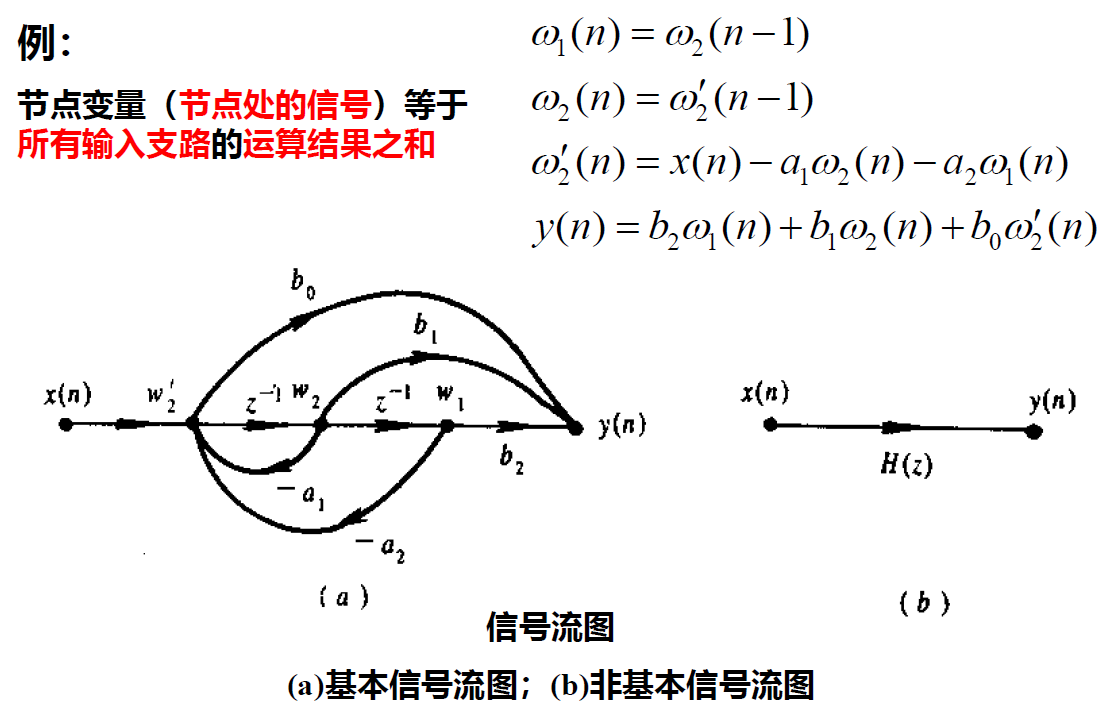
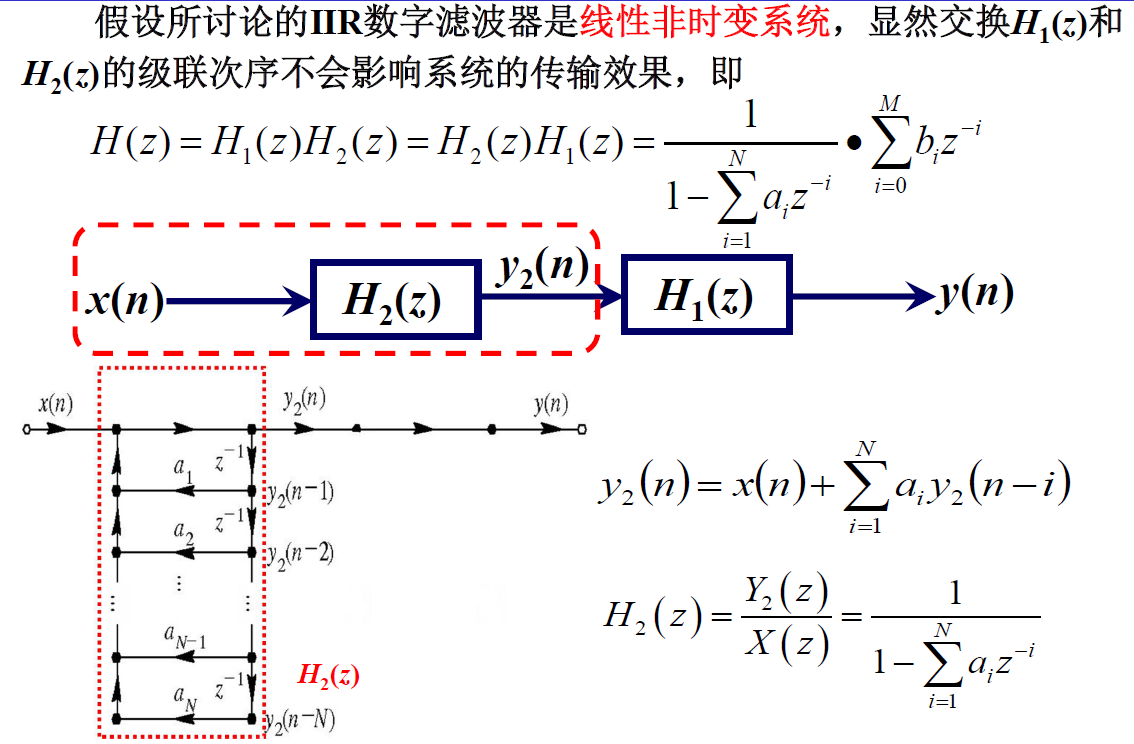
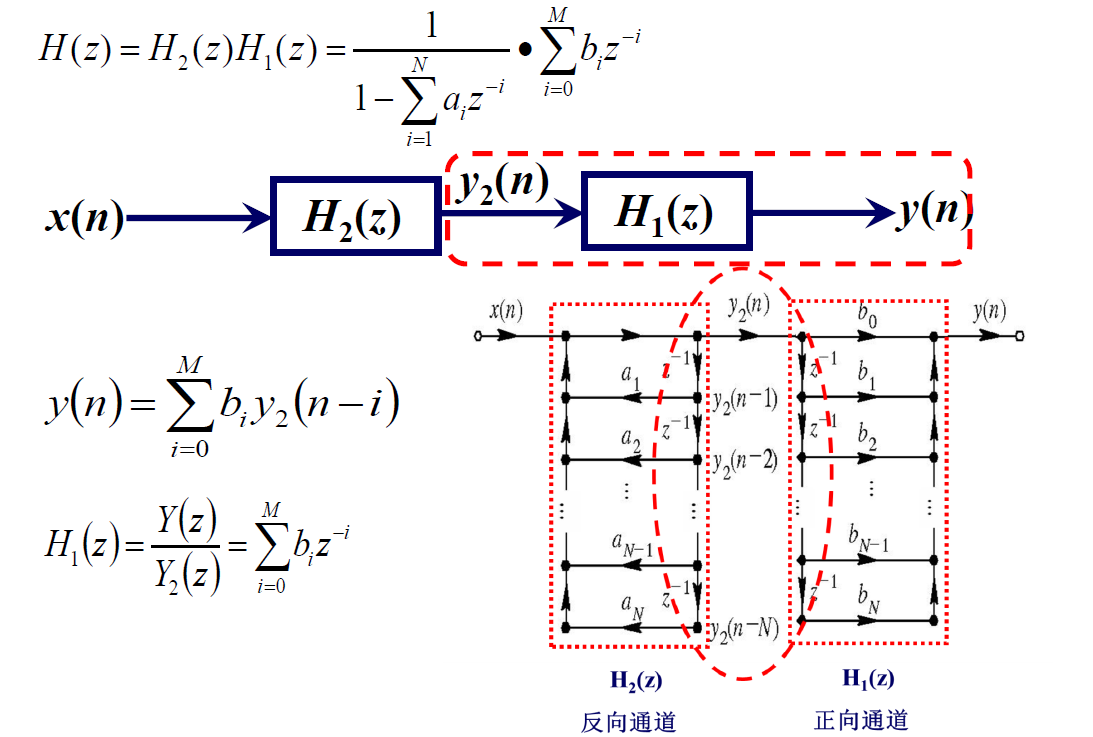
信号流图
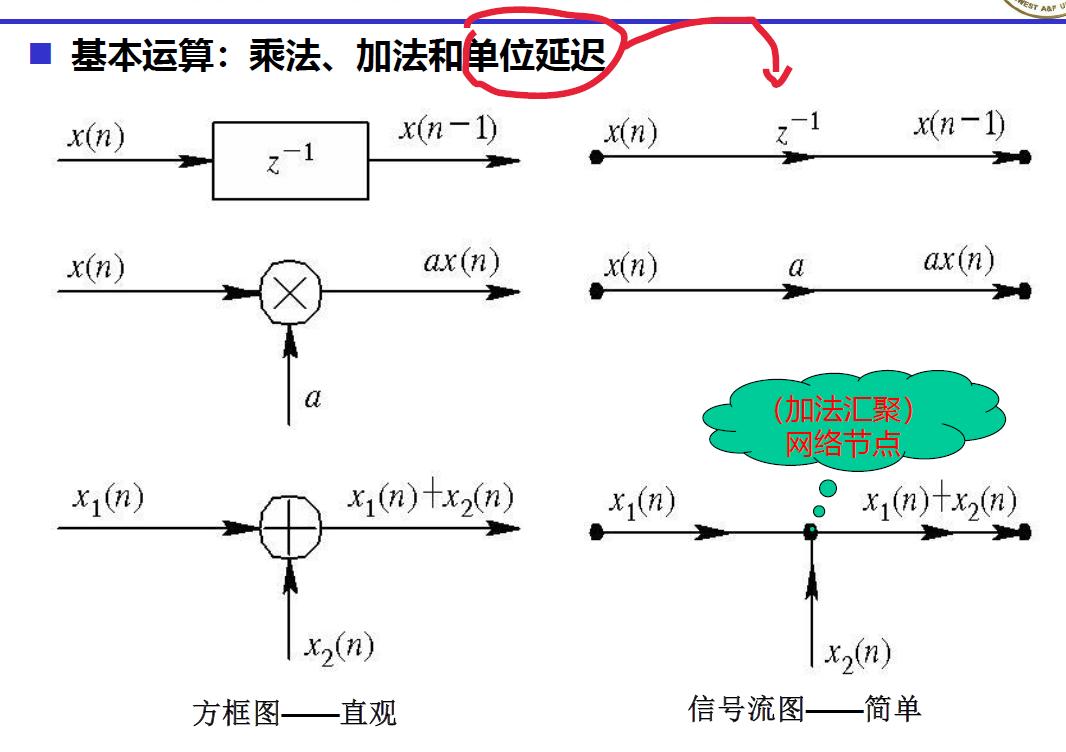
只看输入
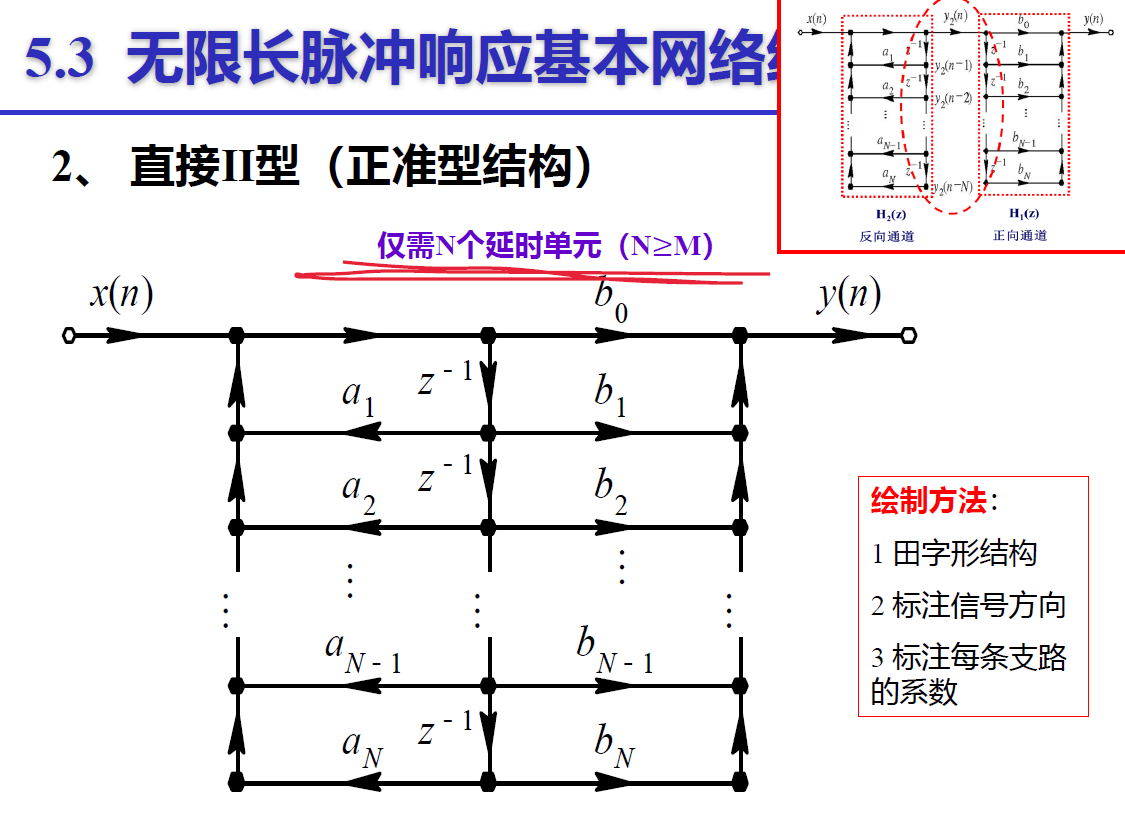
直接型
直接I型
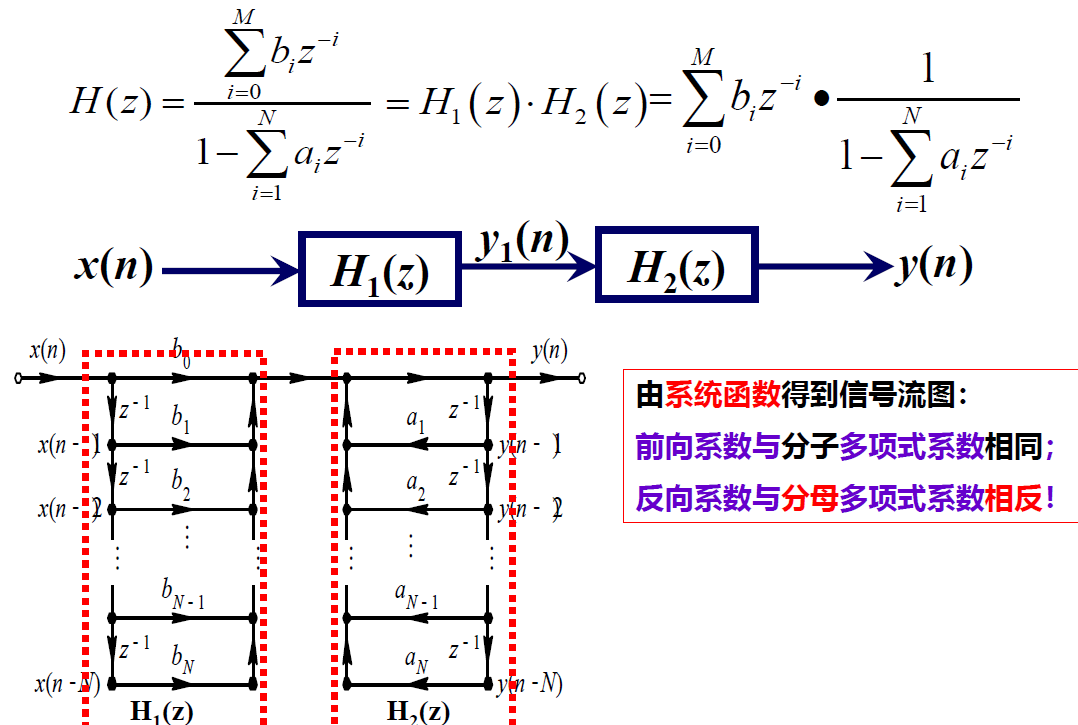
直接II型
直接型例题

级联型
第一级输出直接接第二级输入


级联型例题

并联型
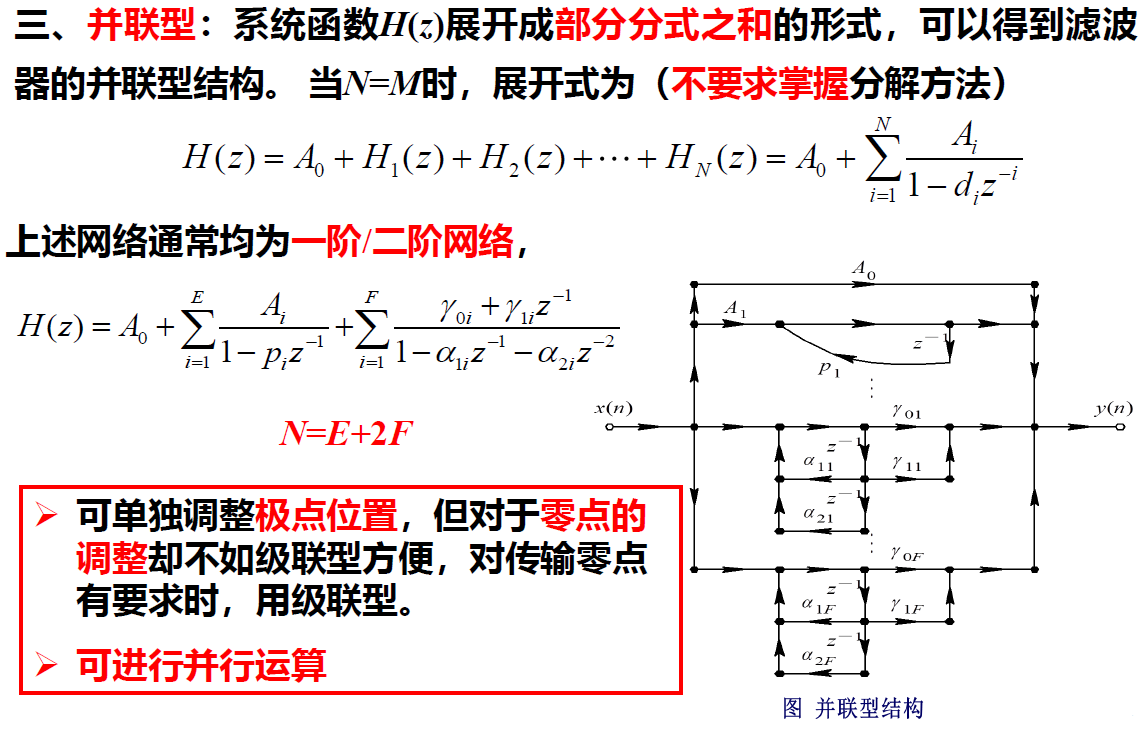
零极点分布图
会画
第六章
滤波器设计步骤

巴特沃斯低通滤波器
参数理解:
\(f_p\):通带截止频率
\(\alpha_p\):通带最大衰减
\(f_s\):阻带截止频率
\(\alpha_s\):阻带最大衰减
做题步骤:
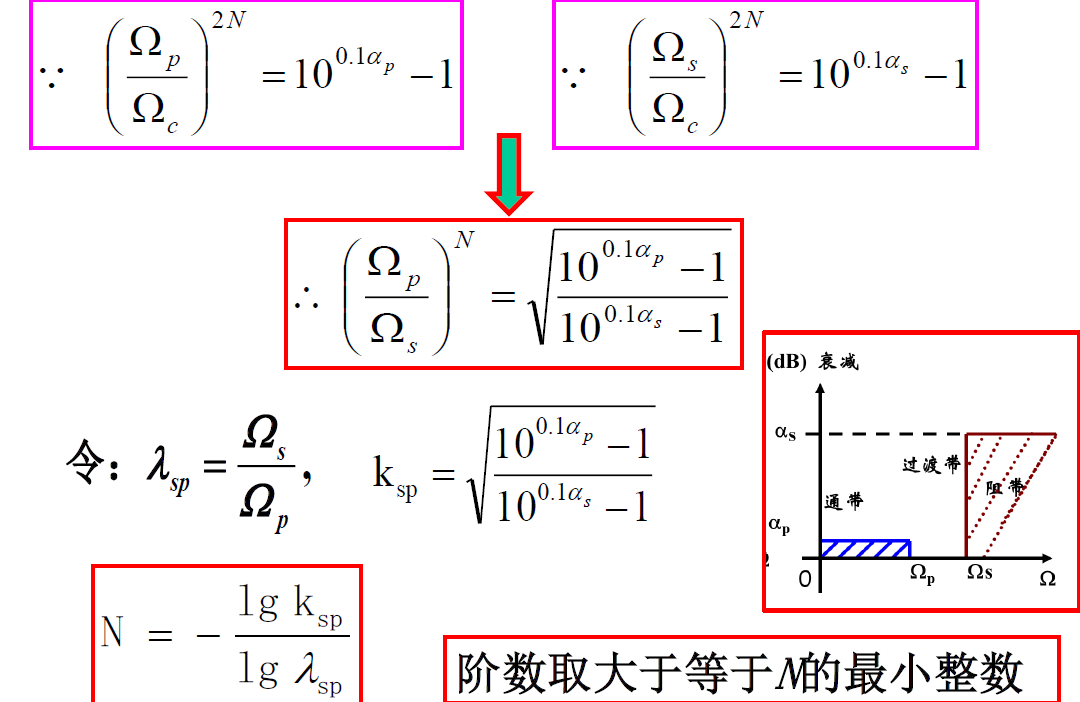
先求\(k_{sp}、\lambda_{sp}、N\)
记法:sp,则分子s分母p \[ \begin{align*} k_{sp}&=\sqrt{\frac{10^{0.1\alpha_s}-1}{10^{0.1\alpha_p}-1}}\\\\ \lambda_{sp}&=\frac{2\pi f_s}{2\pi f_p}=\frac{\Omega_s}{\Omega_p}\\\\ N&=\frac{\lg k_{sp}}{\lg \lambda_{sp}} \end{align*} \] 将N向上取整,得到一个整数
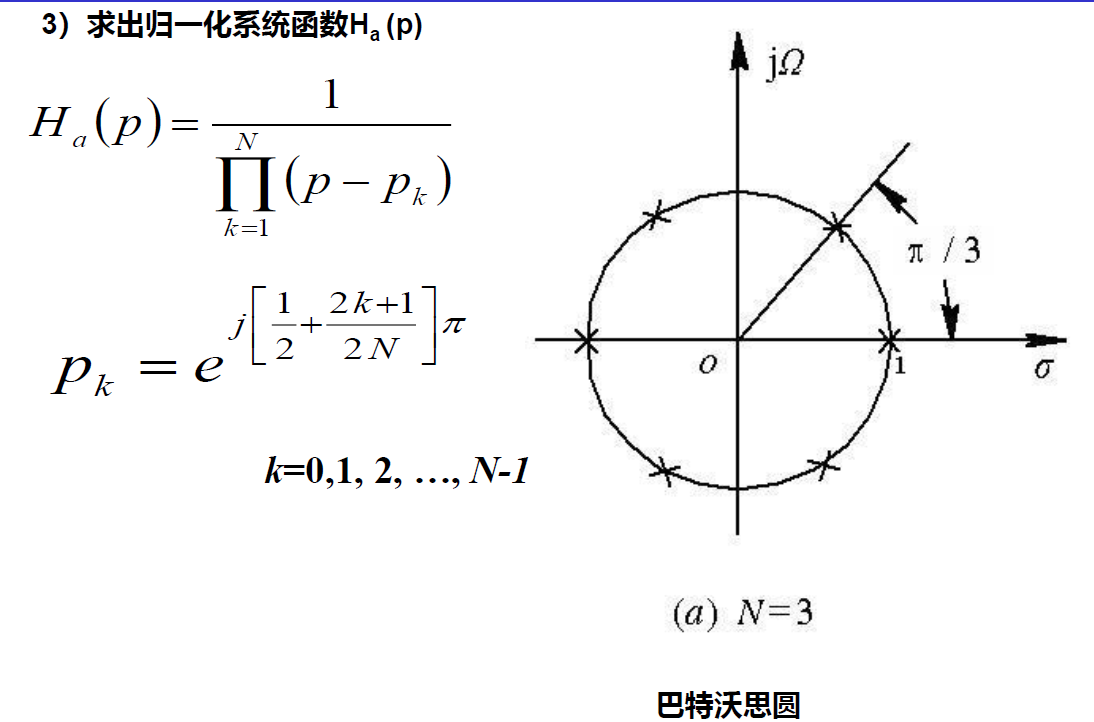
查表,获得极点参数,列出极点

查表,获得归一化系统函数参数\(b_n\),列出归一化系统函数参数,\(b_0,b_1\dots b_{N-1}\)
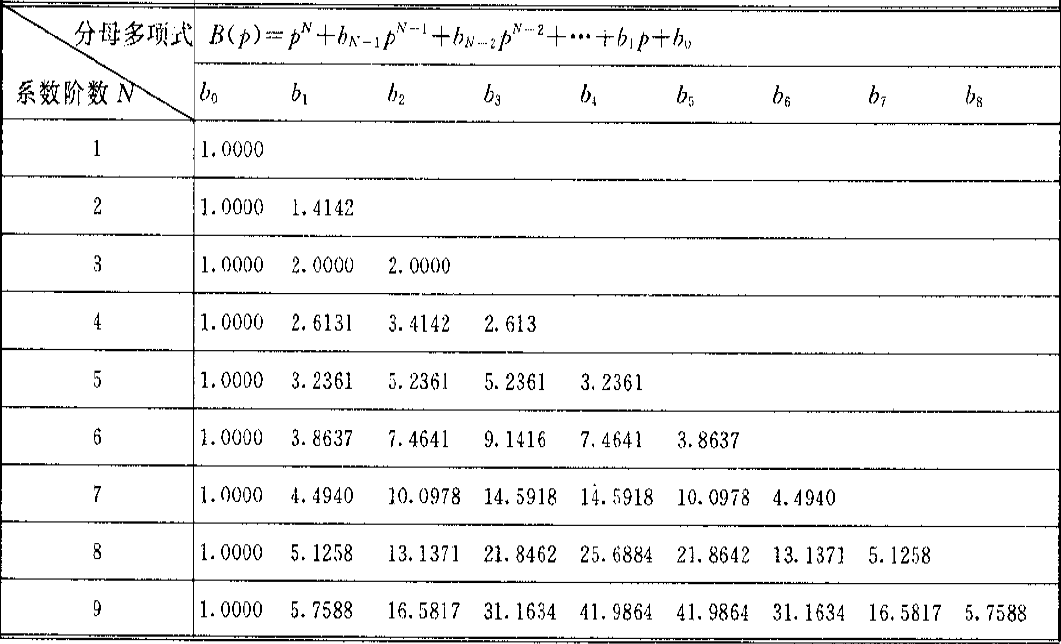
写出归一化低通原型系统函数
\(G_a(p)=\dfrac{1}{p^N+b_{N-1}p^{N-1}+b_{N-2}p^{N-2}+\dots+b_1p^1+b_0}\)
带入N,此时不需要带入b和p
我们学到的内容,做到这一步以后直接查表因式分解
\(H_a(p)=\dfrac{1}{\prod\limits_{k=0}^{N-1}(p-p_k)}\)
网上查的方法:继上一步后
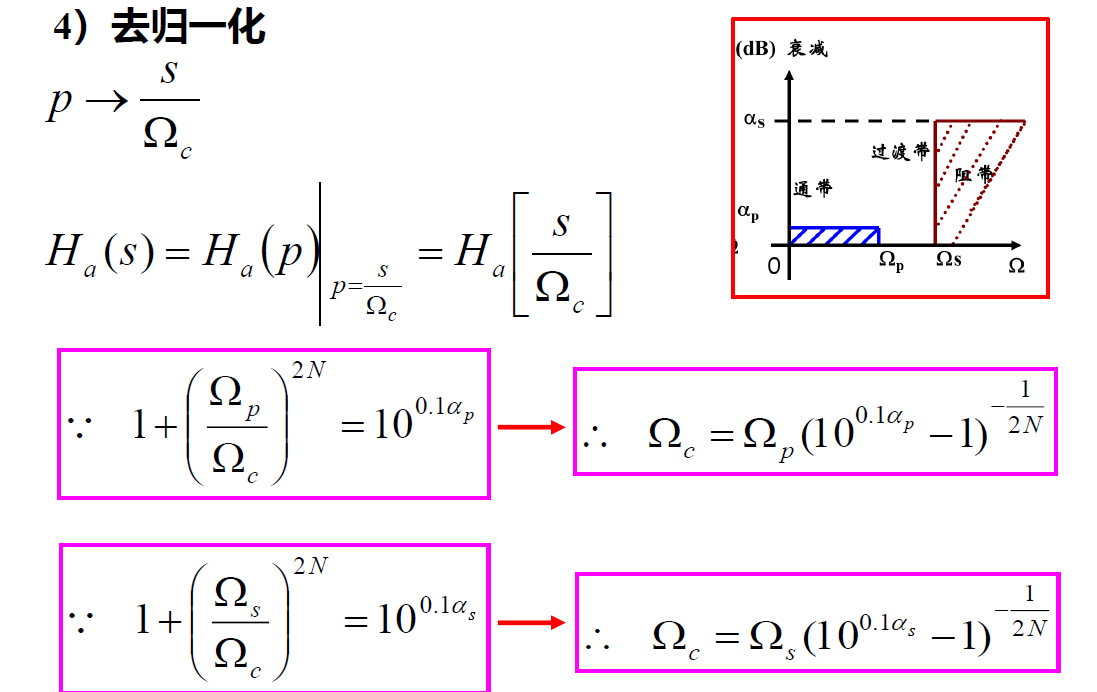
计算\(\Omega{c}\),单位为rad/s
\(\Omega{c}=2\pi f_p(10^{0.1\alpha_p}-1)^{-\frac{1}{2N}}\)
写去归一化,得到结果表达(写成\(H_a(s)\),把\(p=\dfrac{s}{\Omega_c}\)代入)
\(H_a(s)=\dfrac{\Omega_c^N}{s^N+b_{N-1}\Omega_c^1s^{N-1}+b_{N-2}\Omega_c^2s^{N-2}+\dots+b_1\Omega_c^{N-1}s^1+b_0\Omega_c^N}\)
参考:
例题




\[ \begin{align*} 首先计算&k_{sp}、\lambda_{sp}、N\\ k_{sp}&=\sqrt{\frac{10^{0.1\alpha_s}-1}{10^{0.1\alpha_p}-1}}=41.3\\\\ \lambda_{sp}&=\frac{2\pi f_s}{2\pi f_p}=2.4\\\\ N&=\frac{\lg k_{sp}}{\lg \lambda_{sp}}=4.25\\\\ N&向上取整,则N=5\\\\ 再查表,&列出极点:\\ &-0.3090\pm j0.9511\qquad-0.8090\pm j0.5878\qquad-1.0000\\\\ 再查表,&列出b:\\ &b_1=1.0000\qquad b_2=3.2361\qquad b_3=5.2361\qquad b_4=5.2362\qquad b_5=3.2361\\\\ 写出&归一化低通原型系统函数\\ H_a(p)&=\frac{1}{p^N+b_{N-1}p^{N-1}+b_{N-2}p^{N-2}+\dots+b_1p^1+b_0}\\\\ &=\frac{1}{p^5+b_{4}p^{4}+b_{3}p^{3}+b_{2}p^{2}+b_1p^1+b_0}\\\\\\ 查表&因式分解:\\ H_a(p)&=\frac{1}{(p^2+0.6180p+1)(p^2+1.6180p+1)(p+1)}\\\\\\ 求出&\Omega_c:\\ \Omega_c&=2\pi f_p(10^{0.1\alpha_p}-1)^{-\frac{1}{2N}}\\\\ &=10559.8\pi\quad rad/s\\\\ 将p=\frac{s}{\Omega_c}&带入H_a(p)中:\\\\ H_a(s)&=\frac{\Omega_c^5}{s^5+b_{4}\Omega_c^1s^{4}+b_{3}\Omega_c^2s^{3}+b_{2}\Omega_c^3s^{2}+b_1\Omega_c^{4}s^1+b_0\Omega_c^5} \end{align*} \]
IIR数字低通滤波器设计
将\(H_a(s)\)转为\(H(z)\)
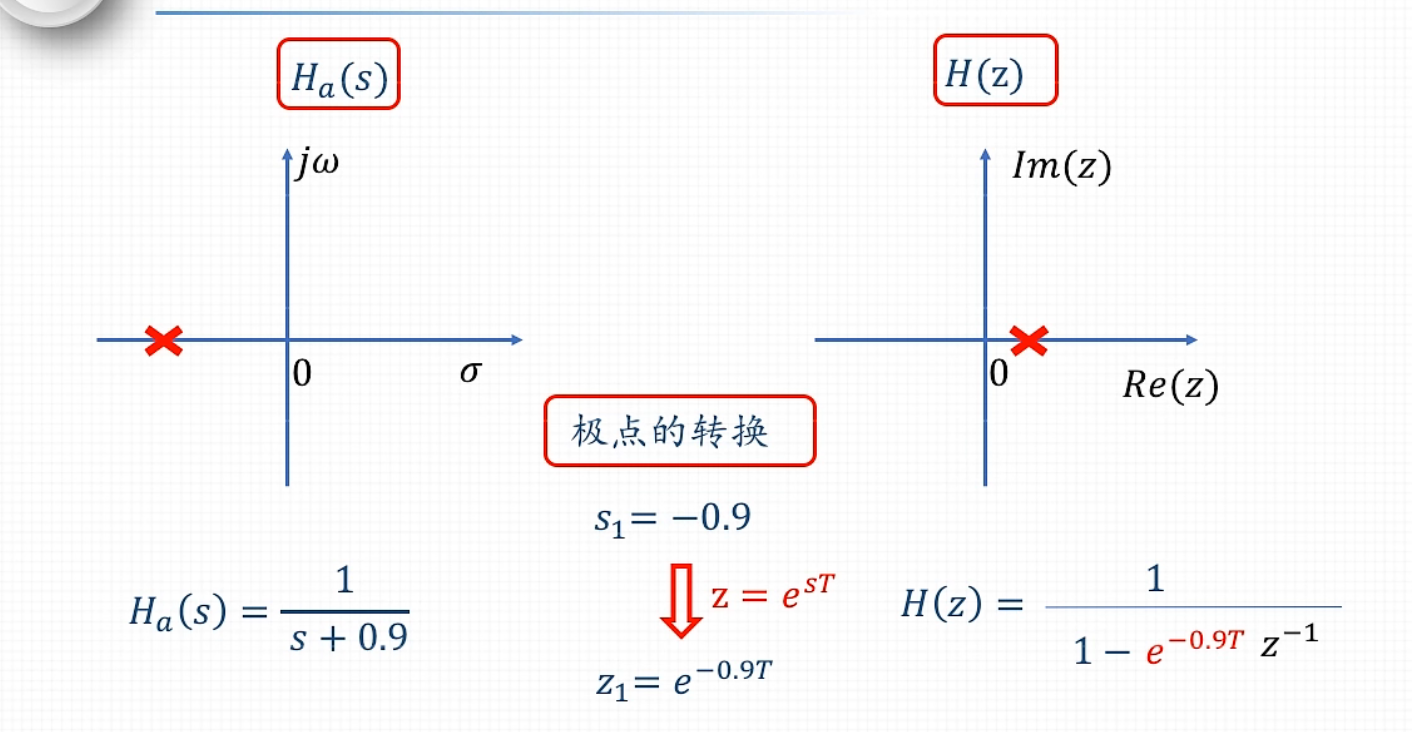
脉冲响应不变法
算出\(H_a(s)\)的极点s,再对s套公式\(z=e^{sT}\)得到z



例题
\(z=e^{sT}\)

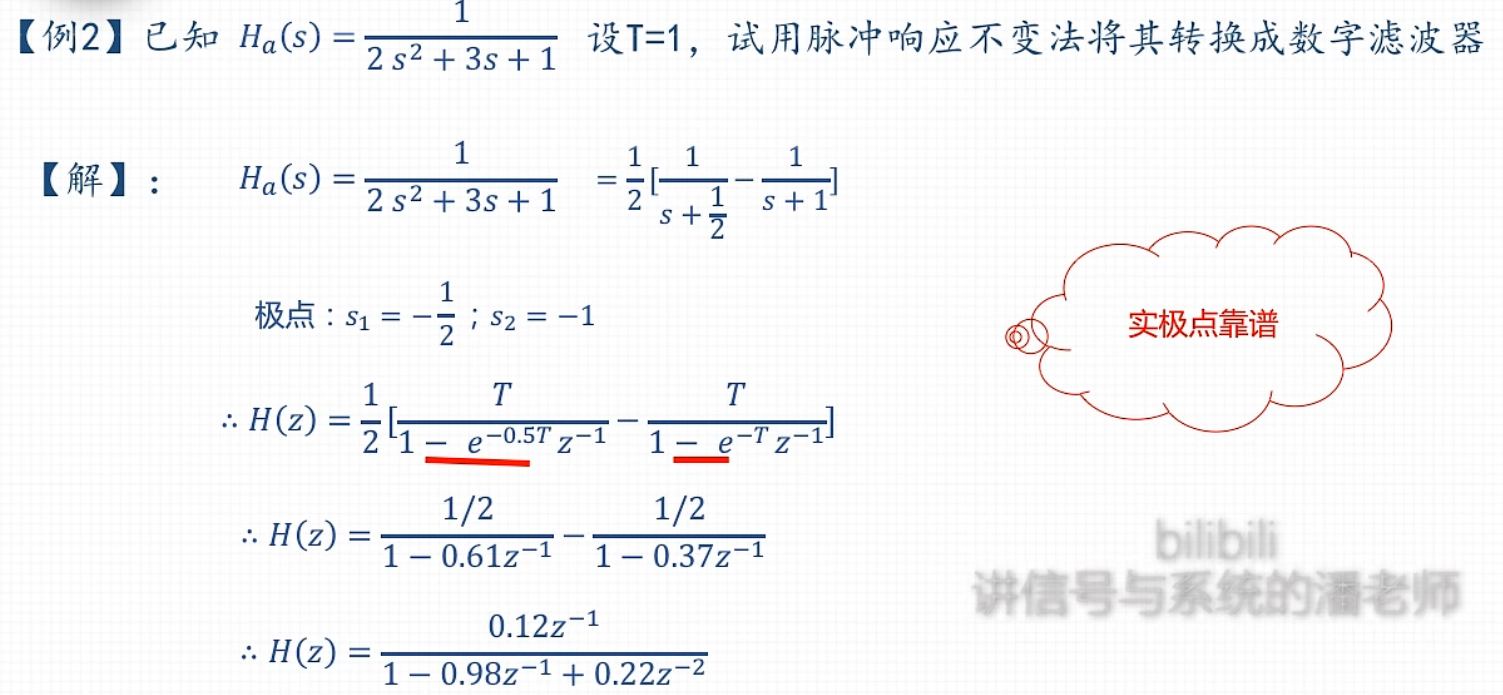
参考:
作业



